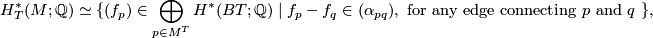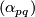GKM manifold
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Definition
Let 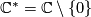 and
and 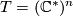 be the complex
be the complex  -torus with
-torus with  . A GKM manifold
. A GKM manifold  is a complex smooth projective variety with an algebraic action of
is a complex smooth projective variety with an algebraic action of  satisfying the following three conditions;
satisfying the following three conditions;
- the fixed point set
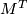 is finite,
is finite,
- the set
 of the complex one-dimensional orbits is finite,
of the complex one-dimensional orbits is finite,
- the action is equivariantly formal, that is, the Leray-Serre cohomology spectral sequence for the Borel construction collapses at
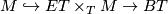
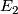 -term.
-term.
The letters `G', `K' and `M' correspond to the first initials of the authors of [Goresky&Kottwitz&MacPherson1998] where GKM manifolds were first introduced.
Let  . Then it is shown in [Goresky&Kottwitz&MacPherson1998] that
. Then it is shown in [Goresky&Kottwitz&MacPherson1998] that 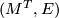 forms an
forms an  -valent simple graph in the sense that the following hold:
-valent simple graph in the sense that the following hold:
- The closure of each orbit
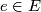 is an embedded
is an embedded 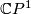 containing exactly two fixed points at the north and the south pole.
containing exactly two fixed points at the north and the south pole.
- At any
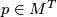 , the closures of
, the closures of  orbits meet.
orbits meet.
For any edge connecting 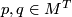 , let
, let 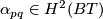 be the weight of the isotropic representation of
be the weight of the isotropic representation of  on
on 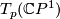 , where
, where 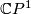 is the corresponding closure of the one-dimensional
is the corresponding closure of the one-dimensional  -orbit. The graph
-orbit. The graph 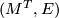 together with this data often referred to as the GKM graph associated to
together with this data often referred to as the GKM graph associated to  . The main theorem in [Goresky&Kottwitz&MacPherson1998] states that the rational
. The main theorem in [Goresky&Kottwitz&MacPherson1998] states that the rational  -equivariant Borel cohomology of
-equivariant Borel cohomology of  ,
, 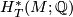 , is described in terms of the GKM graph:
, is described in terms of the GKM graph:
2 Examples
Projective toric manifolds and flag manifolds are examples of GKM manifolds and the above theorem corresponds to the piecewise polynomial description ([Brion&Vergne1997]) and Arabia's description ([Arabia1989]) of the  -equivariant cohomology of those manifolds.
-equivariant cohomology of those manifolds.
3 Further discussion
Several generalisation of the theory are known; for example, [Braden&MacPherson2001] for equivariant intersection homology, [Rosu2003] for equivariant  -theory, [Harada&Henriques&Holm2005] for complex oriented cohomology theories, [Guillemin&Holm2004] for action with non-isolated fixed points, and [Goertsches&Mare2013] for non-abelian group action. For introductory surveys of GKM manifolds, see [Tymoczko2005][Kuroki2009]. The theory of GKM manifolds has applications also in combinatorics. See, for example, [Guillemin&Zara2001][Bolker&Guillemin&Holm2002].
-theory, [Harada&Henriques&Holm2005] for complex oriented cohomology theories, [Guillemin&Holm2004] for action with non-isolated fixed points, and [Goertsches&Mare2013] for non-abelian group action. For introductory surveys of GKM manifolds, see [Tymoczko2005][Kuroki2009]. The theory of GKM manifolds has applications also in combinatorics. See, for example, [Guillemin&Zara2001][Bolker&Guillemin&Holm2002].
4 References
- [Arabia1989] A. Arabia, Cohomologie
 -équivariante de la variété de drapeaux d'un groupe de Kac-Moody, Bull. Soc. Math. France 117 (1989), 129–165. MR1015806 (90i:32042) Zbl 0706.57024
-équivariante de la variété de drapeaux d'un groupe de Kac-Moody, Bull. Soc. Math. France 117 (1989), 129–165. MR1015806 (90i:32042) Zbl 0706.57024
- [Bolker&Guillemin&Holm2002] E. Bolker, V. Guillemin, and T. Holm, How is a graph like a manifold?, (2009). Available at the arXiv:0206103.
- [Braden&MacPherson2001] T. Braden and R. MacPherson, From moment graphs to intersection cohomology, Math. Ann. 321 (2001), 533–551. MR1871967 (2003g:14030) Zbl 1077.14522
- [Brion&Vergne1997] M. Brion and M. Vergne, An equivariant Riemann-Roch theorem for complete, simplicial toric varieties, J. Reine Angew. Math. 482 (1997), 67–92. MR1427657 (98a:14067) Zbl 0862.14006
- [Goertsches&Mare2013] O. Goertsches and A.-L. Mare, Non-abelian GKM theory, to appear in Math. Zeit.
- [Goresky&Kottwitz&MacPherson1998] M. Goresky, R. Kottwitz and R. MacPherson, Equivariant cohomology, Koszul duality, and the localization theorem, Invent. Math. 131 (1998), 25–83. MR1489894 (99c:55009) Zbl 0897.22009
- [Guillemin&Holm2004] V. Guillemin and T. S. Holm, GKM theory for torus actions with nonisolated fixed points, Int. Math. Res. Not. (2004), 2105–2124. MR2064318 (2005d:53136) Zbl 1138.53315
- [Guillemin&Zara2001] V. Guillemin and C. Zara, 1-skeleta, Betti numbers, and equivariant cohomology, Duke Math. J. 107 (2001), 283–349. MR1823050 (2002j:53110) Zbl 1020.57013
- [Harada&Henriques&Holm2005] M. Harada, A. Henriques and T. S. Holm, Computation of generalized equivariant cohomologies of Kac-Moody flag varieties, Adv. Math. 197 (2005), 198–221. MR2166181 (2006h:53086) Zbl 1110.55003
- [Kuroki2009] S. Kuroki, Introduction to GKM theory, Trends in Mathematics (2009).
- [Rosu2003] I. Rosu, Equivariant
 -theory and equivariant cohomology. With an appendix by Allen Knutson and Rosu, Math. Z. 243 (2003), 423–448. MR1970011 (2004f:19011) Zbl 1019.19003
-theory and equivariant cohomology. With an appendix by Allen Knutson and Rosu, Math. Z. 243 (2003), 423–448. MR1970011 (2004f:19011) Zbl 1019.19003
- [Tymoczko2005] J. S. Tymoczko, An introduction to equivariant cohomology and homology, following Goresky, Kottwitz, and MacPherson, Snowbird lectures in algebraic geometry, Contemp. Math., 388, Amer. Math. Soc., Providence, RI (2005), 169–188. MR2182897 (2006m:55019)