Talk:Kervaire-Milnor Braid (Ex)
For starters the braid looks as follows:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \pi_8(O) \ar[dr] \ar@/u\curv/^J[rr] && \Omega_8^{fr} \ar[dr] \ar@/u\curv/[rr] && L_8(\Z) \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& \pi_6(O) \ar[dr] \ar@/u\curv/^J[rr] && \Omega_6^{fr} \ar[dr] \ar@/u\curv/[rr] && L_6(\Z) \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& \pi_{4}(O) \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^s[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar_s[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar^s[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar_s[dr] \ar[ur] & \\ L_9(\Z) \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \pi_7(O) \ar[ur] \ar@/d\curv/_J[rr] &&\Omega_7^{fr} \ar[ur]\ar@/d\curv/[rr] && L_7(\Z) \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && \pi_5(O) \ar[ur] \ar@/d\curv/_J[rr] &&\Omega_5^{fr} \ar[ur]\ar@/d\curv/[rr] && L_5(\Z) }](/images/math/9/f/c/9fc3fa0fd80d53b9a837255efb8349c1.png)
Filling in the 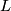 -groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the
-groups (which were computed by Kervaire and Milnor), the homotopy groups of the orthogonal group (which are given by Bott periodicity), the framed bordism groups (which were shown to be the stable stems by Pontryagin and in low dimensions computed by Serre), and the 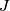 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/d/9/5/d95b6800eee4e6b99c4a23270f0bbd49.png)
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 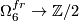 . Using that this is surjective (
. Using that this is surjective (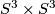 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 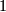 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 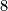 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
The extension at 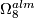 is split since it surjects onto
is split since it surjects onto 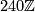 (right lower map) which is free. Clearing this and the obvious
(right lower map) which is free. Clearing this and the obvious 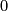 's, we find:
's, we find:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]^{\neq 0}\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@{->>}@/u\curv/[rr] && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr] \ar[ur]^\cong && \Z \times \Z/2 \ar[dr]_{\cdot \pm 240} \ar^{\cdot \pm 28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^\cong && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/b/a/7/ba78997fc728b44a294a64b0974f9e46.png)
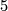 , which is not covered by the usual collary of the
, which is not covered by the usual collary of the 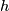 -cobordism theorem. The possibilities for
-cobordism theorem. The possibilities for 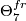 are
are 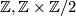 and
and 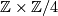 , since it is simultaneously an extension of
, since it is simultaneously an extension of 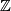 by
by 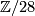 and
and 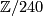 whose common factors are
whose common factors are 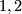 and
and 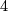 . We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form
. We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form 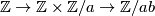
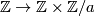 is always given by multiplication with
is always given by multiplication with 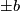 in the first factor. Looking now at the triangle above
in the first factor. Looking now at the triangle above 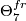 , we find (for some integers
, we find (for some integers 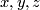 )
)
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z \ar[dr]^{(\cdot \pm \frac {240} i, x)}\ar@{->>}@/u\curv/[rr] & & \Z/28 \\ & \Z \times \Z/i \ar[ur]_{\binom y {z \cdot \frac {240} i}} & }](/images/math/b/5/e/b5e0070ffed2b4c4f4c9c2f83174856a.png)
which is only possible for 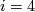 , since the upper map cannot possibly be surjective in the other cases (
, since the upper map cannot possibly be surjective in the other cases ( having a common factor with both
having a common factor with both 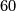 and
and 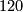 ). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr]^{(1,0)} \ar@/u\curv/[rr]^{(1,0)} && \Z/2 \times \Z/2 \ar[dr]^{\binom {0 \ 0}{0 \ 1}} \ar@/u\curv/[rr] && \Z \ar[dr]^{(60, 1)}\ar@/u\curv/[rr]^{pr} && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^{id} \ar@/u\curv/[rr]^{id} && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr]_{\binom 0 1} \ar[ur]^{id} && \Z \times \Z/2 \ar[dr]_{\cdot 240} \ar^{\cdot 28}[ur] && \Z \times \Z/4 \ar[dr]_{\binom {103}{60}} \ar[ur]^{\binom {12}{21}} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^{id} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Z/2 \ar[ur]_{(0,1)} \ar@/d\curv/[rr] && \Z \ar[ur]_{(7, 0)} \ar@/d\curv/[rr]_ {pr} &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/2/f/c/2fc969ce25938349a6e271c06d55c491.png)
Let's first prove the algebra fact from above: Projecting onto the first factor gives a map of short exact sequences:
![\displaystyle \xymatrix{ \Z \ar[r]^-{(-x,?)} \ar[d]_{x} & \Z \times \Z/a \ar[r] \ar[d]_{\binom 1 0} & \Z/ab \ar[d] \\ \Z \ar[r]_{id} & \Z \ar[r] & 0 }](/images/math/4/7/e/47ef08424ac521a6d9f01e86d4261ddf.png)
The conclusion is then immediate from the snake lemma. The only nontrivial left to prove now is that there is only a single isomorphism class for a diagram of the form
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr] \ar@/u\curv/[rr] & & \Z/28 \\ \Z \ar[ur] \ar[dr] & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur] \ar@/d\curv/[rr] & & \Z/240 }](/images/math/f/6/2/f625357f4e60c4f9e1bf7db191677417.png)
with the obvious exactness properties derived from the braid above. We will convert such a diagram to the one displayed in the braid above in several steps. First, the maps between the 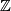 entries are certainly given by multiplication with
entries are certainly given by multiplication with 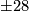 and
and 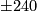 , respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower
, respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower 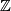 as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps
as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps 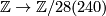 are surjective the isomorphism of braids given by dividing by the image of
are surjective the isomorphism of braids given by dividing by the image of 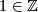 in
in 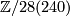 converts these maps into the projections. Switching the sign on the
converts these maps into the projections. Switching the sign on the 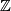 -summand of
-summand of 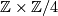 and using the fact from above, we can change the upper map
and using the fact from above, we can change the upper map 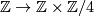 (which is given by
(which is given by 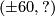 into the
into the 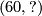 . The lower map will then be determined to be
. The lower map will then be determined to be 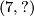 by commutativity of the left square. Our given diagram is thus isomorphic to the following:
by commutativity of the left square. Our given diagram is thus isomorphic to the following:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,?)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,?)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/e/c/1/ec1e69ddaae3d1edc2dfb3236807a7ad.png)
By commutativity of the upper triangle, we also know that the only possibilities for the upper map are 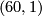 and
and 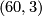 (otherwise the upper map would not be surjective). Multiplying with
(otherwise the upper map would not be surjective). Multiplying with 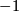 on the
on the 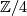 -summand if necessary we can arrange this to be
-summand if necessary we can arrange this to be 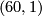 . Now for the fun part: Composing with the shearing isomorphism
. Now for the fun part: Composing with the shearing isomorphism 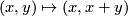 of
of 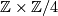 leaves the map
leaves the map 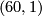 fixed, since
fixed, since 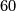 is divisible by
is divisible by 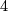 , and changes the map
, and changes the map 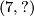 to
to 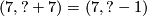 . So using the induced isomorphism of braids we can arrange for
. So using the induced isomorphism of braids we can arrange for 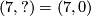 without changing anything fixed before:
without changing anything fixed before:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,1)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,0)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/d/6/a/d6af79bd3c2ef4e1b505f85f91436870.png)
The other two maps are now determined: For the lower triangle to commute we must have the lower right map be 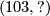 (
(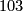 being the multiplicative inverse of
being the multiplicative inverse of 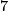 modulo
modulo 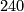 . For the composition with the upper left map to be zero, the second component has to be
. For the composition with the upper left map to be zero, the second component has to be 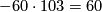 modulo
modulo 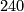 . For other sequence to be exact we need the restriction to
. For other sequence to be exact we need the restriction to 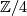 of the unknown map
of the unknown map 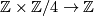 injective (the kernel is torsionfree) so it has to be of the form
injective (the kernel is torsionfree) so it has to be of the form 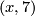 or
or 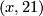 . For the upper triangle to commute one then finds the following congruences modulo
. For the upper triangle to commute one then finds the following congruences modulo  to be solved:
to be solved:
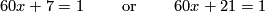
which amounts to finding solutions to
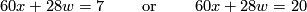
which is obviously impossible in the first case. The solutions modulo  of the second equation are given by
of the second equation are given by 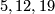 and
and 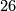 . For the composition with the lower left map to be zero this number has to be divisible by
. For the composition with the lower left map to be zero this number has to be divisible by 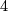 and only
and only 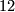 is. This concludes negotiations.
is. This concludes negotiations.
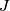 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/d/9/5/d95b6800eee4e6b99c4a23270f0bbd49.png)
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 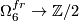 . Using that this is surjective (
. Using that this is surjective (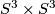 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 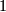 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 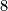 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
The extension at 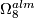 is split since it surjects onto
is split since it surjects onto 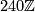 (right lower map) which is free. Clearing this and the obvious
(right lower map) which is free. Clearing this and the obvious 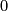 's, we find:
's, we find:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]^{\neq 0}\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@{->>}@/u\curv/[rr] && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr] \ar[ur]^\cong && \Z \times \Z/2 \ar[dr]_{\cdot \pm 240} \ar^{\cdot \pm 28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^\cong && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/b/a/7/ba78997fc728b44a294a64b0974f9e46.png)
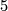 , which is not covered by the usual collary of the
, which is not covered by the usual collary of the 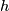 -cobordism theorem. The possibilities for
-cobordism theorem. The possibilities for 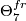 are
are 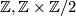 and
and 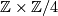 , since it is simultaneously an extension of
, since it is simultaneously an extension of 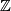 by
by 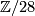 and
and 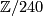 whose common factors are
whose common factors are 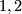 and
and 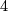 . We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form
. We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form 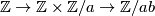
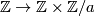 is always given by multiplication with
is always given by multiplication with 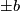 in the first factor. Looking now at the triangle above
in the first factor. Looking now at the triangle above 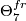 , we find (for some integers
, we find (for some integers 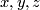 )
)
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z \ar[dr]^{(\cdot \pm \frac {240} i, x)}\ar@{->>}@/u\curv/[rr] & & \Z/28 \\ & \Z \times \Z/i \ar[ur]_{\binom y {z \cdot \frac {240} i}} & }](/images/math/b/5/e/b5e0070ffed2b4c4f4c9c2f83174856a.png)
which is only possible for 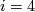 , since the upper map cannot possibly be surjective in the other cases (
, since the upper map cannot possibly be surjective in the other cases ( having a common factor with both
having a common factor with both 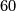 and
and 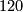 ). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr]^{(1,0)} \ar@/u\curv/[rr]^{(1,0)} && \Z/2 \times \Z/2 \ar[dr]^{\binom {0 \ 0}{0 \ 1}} \ar@/u\curv/[rr] && \Z \ar[dr]^{(60, 1)}\ar@/u\curv/[rr]^{pr} && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^{id} \ar@/u\curv/[rr]^{id} && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr]_{\binom 0 1} \ar[ur]^{id} && \Z \times \Z/2 \ar[dr]_{\cdot 240} \ar^{\cdot 28}[ur] && \Z \times \Z/4 \ar[dr]_{\binom {103}{60}} \ar[ur]^{\binom {12}{21}} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^{id} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Z/2 \ar[ur]_{(0,1)} \ar@/d\curv/[rr] && \Z \ar[ur]_{(7, 0)} \ar@/d\curv/[rr]_ {pr} &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/2/f/c/2fc969ce25938349a6e271c06d55c491.png)
Let's first prove the algebra fact from above: Projecting onto the first factor gives a map of short exact sequences:
![\displaystyle \xymatrix{ \Z \ar[r]^-{(-x,?)} \ar[d]_{x} & \Z \times \Z/a \ar[r] \ar[d]_{\binom 1 0} & \Z/ab \ar[d] \\ \Z \ar[r]_{id} & \Z \ar[r] & 0 }](/images/math/4/7/e/47ef08424ac521a6d9f01e86d4261ddf.png)
The conclusion is then immediate from the snake lemma. The only nontrivial left to prove now is that there is only a single isomorphism class for a diagram of the form
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr] \ar@/u\curv/[rr] & & \Z/28 \\ \Z \ar[ur] \ar[dr] & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur] \ar@/d\curv/[rr] & & \Z/240 }](/images/math/f/6/2/f625357f4e60c4f9e1bf7db191677417.png)
with the obvious exactness properties derived from the braid above. We will convert such a diagram to the one displayed in the braid above in several steps. First, the maps between the 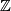 entries are certainly given by multiplication with
entries are certainly given by multiplication with 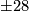 and
and 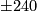 , respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower
, respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower 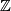 as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps
as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps 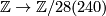 are surjective the isomorphism of braids given by dividing by the image of
are surjective the isomorphism of braids given by dividing by the image of 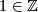 in
in 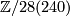 converts these maps into the projections. Switching the sign on the
converts these maps into the projections. Switching the sign on the 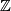 -summand of
-summand of 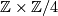 and using the fact from above, we can change the upper map
and using the fact from above, we can change the upper map 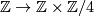 (which is given by
(which is given by 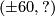 into the
into the 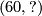 . The lower map will then be determined to be
. The lower map will then be determined to be 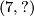 by commutativity of the left square. Our given diagram is thus isomorphic to the following:
by commutativity of the left square. Our given diagram is thus isomorphic to the following:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,?)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,?)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/e/c/1/ec1e69ddaae3d1edc2dfb3236807a7ad.png)
By commutativity of the upper triangle, we also know that the only possibilities for the upper map are 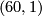 and
and 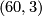 (otherwise the upper map would not be surjective). Multiplying with
(otherwise the upper map would not be surjective). Multiplying with 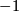 on the
on the 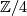 -summand if necessary we can arrange this to be
-summand if necessary we can arrange this to be 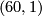 . Now for the fun part: Composing with the shearing isomorphism
. Now for the fun part: Composing with the shearing isomorphism 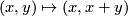 of
of 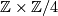 leaves the map
leaves the map 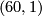 fixed, since
fixed, since 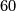 is divisible by
is divisible by 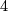 , and changes the map
, and changes the map 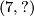 to
to 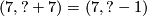 . So using the induced isomorphism of braids we can arrange for
. So using the induced isomorphism of braids we can arrange for 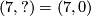 without changing anything fixed before:
without changing anything fixed before:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,1)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,0)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/d/6/a/d6af79bd3c2ef4e1b505f85f91436870.png)
The other two maps are now determined: For the lower triangle to commute we must have the lower right map be 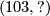 (
(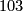 being the multiplicative inverse of
being the multiplicative inverse of 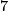 modulo
modulo 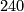 . For the composition with the upper left map to be zero, the second component has to be
. For the composition with the upper left map to be zero, the second component has to be 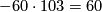 modulo
modulo 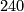 . For other sequence to be exact we need the restriction to
. For other sequence to be exact we need the restriction to 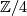 of the unknown map
of the unknown map 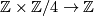 injective (the kernel is torsionfree) so it has to be of the form
injective (the kernel is torsionfree) so it has to be of the form 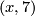 or
or 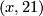 . For the upper triangle to commute one then finds the following congruences modulo
. For the upper triangle to commute one then finds the following congruences modulo  to be solved:
to be solved:
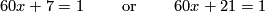
which amounts to finding solutions to
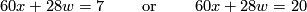
which is obviously impossible in the first case. The solutions modulo  of the second equation are given by
of the second equation are given by 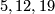 and
and 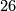 . For the composition with the lower left map to be zero this number has to be divisible by
. For the composition with the lower left map to be zero this number has to be divisible by 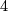 and only
and only 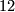 is. This concludes negotiations.
is. This concludes negotiations.
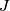 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/d/9/5/d95b6800eee4e6b99c4a23270f0bbd49.png)
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 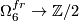 . Using that this is surjective (
. Using that this is surjective (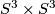 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 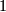 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 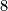 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
The extension at 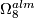 is split since it surjects onto
is split since it surjects onto 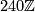 (right lower map) which is free. Clearing this and the obvious
(right lower map) which is free. Clearing this and the obvious 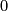 's, we find:
's, we find:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]^{\neq 0}\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@{->>}@/u\curv/[rr] && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr] \ar[ur]^\cong && \Z \times \Z/2 \ar[dr]_{\cdot \pm 240} \ar^{\cdot \pm 28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^\cong && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/b/a/7/ba78997fc728b44a294a64b0974f9e46.png)
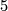 , which is not covered by the usual collary of the
, which is not covered by the usual collary of the 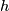 -cobordism theorem. The possibilities for
-cobordism theorem. The possibilities for 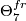 are
are 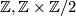 and
and 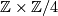 , since it is simultaneously an extension of
, since it is simultaneously an extension of 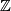 by
by 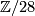 and
and 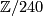 whose common factors are
whose common factors are 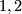 and
and 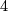 . We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form
. We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form 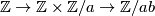
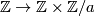 is always given by multiplication with
is always given by multiplication with 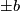 in the first factor. Looking now at the triangle above
in the first factor. Looking now at the triangle above 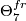 , we find (for some integers
, we find (for some integers 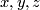 )
)
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z \ar[dr]^{(\cdot \pm \frac {240} i, x)}\ar@{->>}@/u\curv/[rr] & & \Z/28 \\ & \Z \times \Z/i \ar[ur]_{\binom y {z \cdot \frac {240} i}} & }](/images/math/b/5/e/b5e0070ffed2b4c4f4c9c2f83174856a.png)
which is only possible for 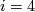 , since the upper map cannot possibly be surjective in the other cases (
, since the upper map cannot possibly be surjective in the other cases ( having a common factor with both
having a common factor with both 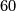 and
and 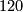 ). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr]^{(1,0)} \ar@/u\curv/[rr]^{(1,0)} && \Z/2 \times \Z/2 \ar[dr]^{\binom {0 \ 0}{0 \ 1}} \ar@/u\curv/[rr] && \Z \ar[dr]^{(60, 1)}\ar@/u\curv/[rr]^{pr} && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^{id} \ar@/u\curv/[rr]^{id} && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr]_{\binom 0 1} \ar[ur]^{id} && \Z \times \Z/2 \ar[dr]_{\cdot 240} \ar^{\cdot 28}[ur] && \Z \times \Z/4 \ar[dr]_{\binom {103}{60}} \ar[ur]^{\binom {12}{21}} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^{id} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Z/2 \ar[ur]_{(0,1)} \ar@/d\curv/[rr] && \Z \ar[ur]_{(7, 0)} \ar@/d\curv/[rr]_ {pr} &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/2/f/c/2fc969ce25938349a6e271c06d55c491.png)
Let's first prove the algebra fact from above: Projecting onto the first factor gives a map of short exact sequences:
![\displaystyle \xymatrix{ \Z \ar[r]^-{(-x,?)} \ar[d]_{x} & \Z \times \Z/a \ar[r] \ar[d]_{\binom 1 0} & \Z/ab \ar[d] \\ \Z \ar[r]_{id} & \Z \ar[r] & 0 }](/images/math/4/7/e/47ef08424ac521a6d9f01e86d4261ddf.png)
The conclusion is then immediate from the snake lemma. The only nontrivial left to prove now is that there is only a single isomorphism class for a diagram of the form
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr] \ar@/u\curv/[rr] & & \Z/28 \\ \Z \ar[ur] \ar[dr] & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur] \ar@/d\curv/[rr] & & \Z/240 }](/images/math/f/6/2/f625357f4e60c4f9e1bf7db191677417.png)
with the obvious exactness properties derived from the braid above. We will convert such a diagram to the one displayed in the braid above in several steps. First, the maps between the 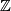 entries are certainly given by multiplication with
entries are certainly given by multiplication with 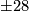 and
and 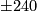 , respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower
, respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower 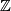 as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps
as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps 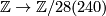 are surjective the isomorphism of braids given by dividing by the image of
are surjective the isomorphism of braids given by dividing by the image of 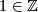 in
in 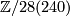 converts these maps into the projections. Switching the sign on the
converts these maps into the projections. Switching the sign on the 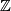 -summand of
-summand of 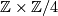 and using the fact from above, we can change the upper map
and using the fact from above, we can change the upper map 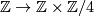 (which is given by
(which is given by 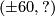 into the
into the 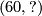 . The lower map will then be determined to be
. The lower map will then be determined to be 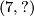 by commutativity of the left square. Our given diagram is thus isomorphic to the following:
by commutativity of the left square. Our given diagram is thus isomorphic to the following:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,?)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,?)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/e/c/1/ec1e69ddaae3d1edc2dfb3236807a7ad.png)
By commutativity of the upper triangle, we also know that the only possibilities for the upper map are 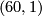 and
and 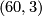 (otherwise the upper map would not be surjective). Multiplying with
(otherwise the upper map would not be surjective). Multiplying with 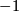 on the
on the 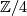 -summand if necessary we can arrange this to be
-summand if necessary we can arrange this to be 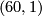 . Now for the fun part: Composing with the shearing isomorphism
. Now for the fun part: Composing with the shearing isomorphism 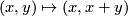 of
of 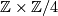 leaves the map
leaves the map 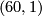 fixed, since
fixed, since 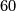 is divisible by
is divisible by 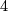 , and changes the map
, and changes the map 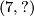 to
to 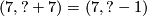 . So using the induced isomorphism of braids we can arrange for
. So using the induced isomorphism of braids we can arrange for 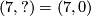 without changing anything fixed before:
without changing anything fixed before:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,1)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,0)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/d/6/a/d6af79bd3c2ef4e1b505f85f91436870.png)
The other two maps are now determined: For the lower triangle to commute we must have the lower right map be 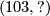 (
(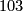 being the multiplicative inverse of
being the multiplicative inverse of 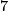 modulo
modulo 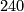 . For the composition with the upper left map to be zero, the second component has to be
. For the composition with the upper left map to be zero, the second component has to be 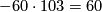 modulo
modulo 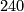 . For other sequence to be exact we need the restriction to
. For other sequence to be exact we need the restriction to 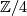 of the unknown map
of the unknown map 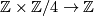 injective (the kernel is torsionfree) so it has to be of the form
injective (the kernel is torsionfree) so it has to be of the form 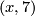 or
or 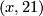 . For the upper triangle to commute one then finds the following congruences modulo
. For the upper triangle to commute one then finds the following congruences modulo  to be solved:
to be solved:
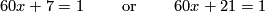
which amounts to finding solutions to
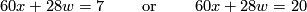
which is obviously impossible in the first case. The solutions modulo  of the second equation are given by
of the second equation are given by 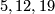 and
and 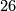 . For the composition with the lower left map to be zero this number has to be divisible by
. For the composition with the lower left map to be zero this number has to be divisible by 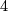 and only
and only 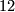 is. This concludes negotiations.
is. This concludes negotiations.
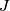 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/d/9/5/d95b6800eee4e6b99c4a23270f0bbd49.png)
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 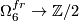 . Using that this is surjective (
. Using that this is surjective (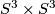 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 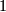 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 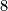 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
The extension at 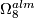 is split since it surjects onto
is split since it surjects onto 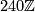 (right lower map) which is free. Clearing this and the obvious
(right lower map) which is free. Clearing this and the obvious  's, we find:
's, we find:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]^{\neq 0}\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@{->>}@/u\curv/[rr] && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr] \ar[ur]^\cong && \Z \times \Z/2 \ar[dr]_{\cdot \pm 240} \ar^{\cdot \pm 28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^\cong && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/b/a/7/ba78997fc728b44a294a64b0974f9e46.png)
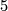 , which is not covered by the usual collary of the
, which is not covered by the usual collary of the 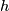 -cobordism theorem. The possibilities for
-cobordism theorem. The possibilities for 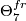 are
are 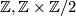 and
and 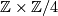 , since it is simultaneously an extension of
, since it is simultaneously an extension of 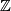 by
by 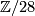 and
and 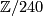 whose common factors are
whose common factors are 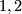 and
and 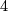 . We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form
. We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form 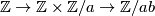
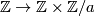 is always given by multiplication with
is always given by multiplication with 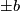 in the first factor. Looking now at the triangle above
in the first factor. Looking now at the triangle above 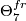 , we find (for some integers
, we find (for some integers 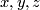 )
)
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z \ar[dr]^{(\cdot \pm \frac {240} i, x)}\ar@{->>}@/u\curv/[rr] & & \Z/28 \\ & \Z \times \Z/i \ar[ur]_{\binom y {z \cdot \frac {240} i}} & }](/images/math/b/5/e/b5e0070ffed2b4c4f4c9c2f83174856a.png)
which is only possible for 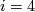 , since the upper map cannot possibly be surjective in the other cases (
, since the upper map cannot possibly be surjective in the other cases ( having a common factor with both
having a common factor with both 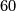 and
and 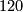 ). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr]^{(1,0)} \ar@/u\curv/[rr]^{(1,0)} && \Z/2 \times \Z/2 \ar[dr]^{\binom {0 \ 0}{0 \ 1}} \ar@/u\curv/[rr] && \Z \ar[dr]^{(60, 1)}\ar@/u\curv/[rr]^{pr} && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^{id} \ar@/u\curv/[rr]^{id} && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr]_{\binom 0 1} \ar[ur]^{id} && \Z \times \Z/2 \ar[dr]_{\cdot 240} \ar^{\cdot 28}[ur] && \Z \times \Z/4 \ar[dr]_{\binom {103}{60}} \ar[ur]^{\binom {12}{21}} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^{id} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Z/2 \ar[ur]_{(0,1)} \ar@/d\curv/[rr] && \Z \ar[ur]_{(7, 0)} \ar@/d\curv/[rr]_ {pr} &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/2/f/c/2fc969ce25938349a6e271c06d55c491.png)
Let's first prove the algebra fact from above: Projecting onto the first factor gives a map of short exact sequences:
![\displaystyle \xymatrix{ \Z \ar[r]^-{(-x,?)} \ar[d]_{x} & \Z \times \Z/a \ar[r] \ar[d]_{\binom 1 0} & \Z/ab \ar[d] \\ \Z \ar[r]_{id} & \Z \ar[r] & 0 }](/images/math/4/7/e/47ef08424ac521a6d9f01e86d4261ddf.png)
The conclusion is then immediate from the snake lemma. The only nontrivial left to prove now is that there is only a single isomorphism class for a diagram of the form
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr] \ar@/u\curv/[rr] & & \Z/28 \\ \Z \ar[ur] \ar[dr] & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur] \ar@/d\curv/[rr] & & \Z/240 }](/images/math/f/6/2/f625357f4e60c4f9e1bf7db191677417.png)
with the obvious exactness properties derived from the braid above. We will convert such a diagram to the one displayed in the braid above in several steps. First, the maps between the 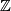 entries are certainly given by multiplication with
entries are certainly given by multiplication with 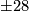 and
and 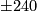 , respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower
, respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower 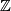 as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps
as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps 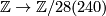 are surjective the isomorphism of braids given by dividing by the image of
are surjective the isomorphism of braids given by dividing by the image of 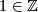 in
in 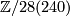 converts these maps into the projections. Switching the sign on the
converts these maps into the projections. Switching the sign on the 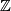 -summand of
-summand of 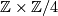 and using the fact from above, we can change the upper map
and using the fact from above, we can change the upper map 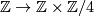 (which is given by
(which is given by 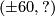 into the
into the 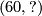 . The lower map will then be determined to be
. The lower map will then be determined to be 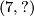 by commutativity of the left square. Our given diagram is thus isomorphic to the following:
by commutativity of the left square. Our given diagram is thus isomorphic to the following:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,?)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,?)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/e/c/1/ec1e69ddaae3d1edc2dfb3236807a7ad.png)
By commutativity of the upper triangle, we also know that the only possibilities for the upper map are 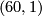 and
and 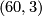 (otherwise the upper map would not be surjective). Multiplying with
(otherwise the upper map would not be surjective). Multiplying with 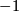 on the
on the 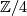 -summand if necessary we can arrange this to be
-summand if necessary we can arrange this to be 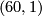 . Now for the fun part: Composing with the shearing isomorphism
. Now for the fun part: Composing with the shearing isomorphism 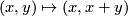 of
of 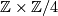 leaves the map
leaves the map 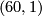 fixed, since
fixed, since 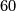 is divisible by
is divisible by 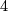 , and changes the map
, and changes the map 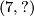 to
to 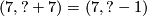 . So using the induced isomorphism of braids we can arrange for
. So using the induced isomorphism of braids we can arrange for 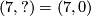 without changing anything fixed before:
without changing anything fixed before:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,1)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,0)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/d/6/a/d6af79bd3c2ef4e1b505f85f91436870.png)
The other two maps are now determined: For the lower triangle to commute we must have the lower right map be 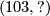 (
(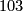 being the multiplicative inverse of
being the multiplicative inverse of 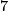 modulo
modulo 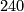 . For the composition with the upper left map to be zero, the second component has to be
. For the composition with the upper left map to be zero, the second component has to be 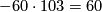 modulo
modulo 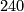 . For other sequence to be exact we need the restriction to
. For other sequence to be exact we need the restriction to 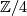 of the unknown map
of the unknown map 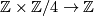 injective (the kernel is torsionfree) so it has to be of the form
injective (the kernel is torsionfree) so it has to be of the form 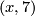 or
or 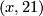 . For the upper triangle to commute one then finds the following congruences modulo
. For the upper triangle to commute one then finds the following congruences modulo  to be solved:
to be solved:
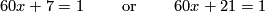
which amounts to finding solutions to
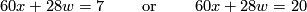
which is obviously impossible in the first case. The solutions modulo  of the second equation are given by
of the second equation are given by 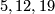 and
and 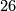 . For the composition with the lower left map to be zero this number has to be divisible by
. For the composition with the lower left map to be zero this number has to be divisible by 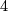 and only
and only 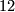 is. This concludes negotiations.
is. This concludes negotiations.
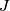 -homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
-homomorphism (which was computed by Adams and Quillen, but can be computed by hand in low dimensions) we arrive at
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr] && \Z \ar@{^{(}->}[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr] \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_8 \ar[dr] \ar^{sign}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_6 \ar[dr] \ar[ur] && \Theta_{5}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/d/9/5/d95b6800eee4e6b99c4a23270f0bbd49.png)
where we have used  to denote the map induced by the Kervaire invariant
to denote the map induced by the Kervaire invariant 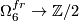 . Using that this is surjective (
. Using that this is surjective (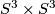 with its Lie-group framing has Kervaire-invariant
with its Lie-group framing has Kervaire-invariant 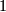 )
and the fact that the signature of an almost framed
)
and the fact that the signature of an almost framed 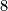 -manifold is divisible by
-manifold is divisible by  (and
(and  is actually the signature of ???), we obtain the following maps:
is actually the signature of ???), we obtain the following maps:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@/u\curv/[rr] &&\Theta_7 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]^0\ar@/u\curv/[rr] &&\Theta_5 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Theta_{8}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_8 \ar[dr] \ar^{28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && \Omega^{alm}_7 \ar[dr] \ar[ur] && \Theta_{6}^{fr} \ar[dr]_\cong \ar@{^{(}->}[ur]^0 && \Omega^{alm}_6 \ar[dr] \ar[ur]^\cong && \Theta_{5}^{fr} \ar[dr] \ar[ur]^\cong && \Omega^{alm}_5 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]_0\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_6 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/9/0/7/9070dd1ce3e34b65b859bfa34ac00927.png)
The extension at 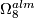 is split since it surjects onto
is split since it surjects onto 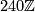 (right lower map) which is free. Clearing this and the obvious
(right lower map) which is free. Clearing this and the obvious 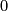 's, we find:
's, we find:
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar@{^{(}->}[dr] \ar@{^{(}->}@/u\curv/[rr] && \Z/2 \times \Z/2 \ar[dr]^{\neq 0}\ar@/u\curv/[rr]^0 && \Z \ar[dr]\ar@{->>}@/u\curv/[rr] && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^\cong \ar@/u\curv/[rr]^\cong && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr] \ar[ur]^\cong && \Z \times \Z/2 \ar[dr]_{\cdot \pm 240} \ar^{\cdot \pm 28}[ur] && \Theta_{7}^{fr} \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^\cong && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Theta_8 \ar[ur] \ar@/d\curv/[rr] && \Z \ar[ur] \ar@{->>}@/d\curv/[rr] &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/b/a/7/ba78997fc728b44a294a64b0974f9e46.png)
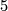 , which is not covered by the usual collary of the
, which is not covered by the usual collary of the 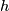 -cobordism theorem. The possibilities for
-cobordism theorem. The possibilities for 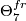 are
are 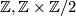 and
and 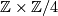 , since it is simultaneously an extension of
, since it is simultaneously an extension of 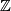 by
by 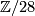 and
and 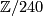 whose common factors are
whose common factors are 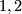 and
and 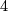 . We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form
. We now claim the following facts from algebra, which we prove after giving the final braid: In an extension of the form 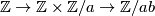
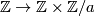 is always given by multiplication with
is always given by multiplication with 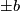 in the first factor. Looking now at the triangle above
in the first factor. Looking now at the triangle above 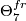 , we find (for some integers
, we find (for some integers 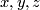 )
)
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z \ar[dr]^{(\cdot \pm \frac {240} i, x)}\ar@{->>}@/u\curv/[rr] & & \Z/28 \\ & \Z \times \Z/i \ar[ur]_{\binom y {z \cdot \frac {240} i}} & }](/images/math/b/5/e/b5e0070ffed2b4c4f4c9c2f83174856a.png)
which is only possible for 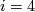 , since the upper map cannot possibly be surjective in the other cases (
, since the upper map cannot possibly be surjective in the other cases ( having a common factor with both
having a common factor with both 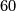 and
and 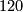 ). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
). With this as input we claim that there is a unique isomorphism class of braids left and it looks as follows (proof given below):
![\displaystyle \def\curv{1.5pc} \xymatrix{ \Z/2 \ar[dr]^{(1,0)} \ar@/u\curv/[rr]^{(1,0)} && \Z/2 \times \Z/2 \ar[dr]^{\binom {0 \ 0}{0 \ 1}} \ar@/u\curv/[rr] && \Z \ar[dr]^{(60, 1)}\ar@/u\curv/[rr]^{pr} && \Z/28 \ar@{->>}[dr]\ar@/u\curv/[rr]&& 0 \ar[dr] \ar@/u\curv/[rr] && \Z/2 \ar[dr]^{id} \ar@/u\curv/[rr]^{id} && \Z/2 \ar[dr]\ar@/u\curv/[rr] &&0 \ar[dr]\ar@/u\curv/[rr]&& 0 \\ & \Z/2 \times \Z/2 \ar[dr]_{\binom 0 1} \ar[ur]^{id} && \Z \times \Z/2 \ar[dr]_{\cdot 240} \ar^{\cdot 28}[ur] && \Z \times \Z/4 \ar[dr]_{\binom {103}{60}} \ar[ur]^{\binom {12}{21}} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] && \Z/2 \ar[dr] \ar[ur]^{id} && 0 \ar[dr] \ar[ur] && 0 \ar[dr] \ar[ur] & \\ 0 \ar[ur] \ar@/d\curv/[rr] && \Z/2 \ar[ur]_{(0,1)} \ar@/d\curv/[rr] && \Z \ar[ur]_{(7, 0)} \ar@/d\curv/[rr]_ {pr} &&\Z/240 \ar[ur]\ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] && 0 \ar[ur] \ar@/d\curv/[rr] &&0 \ar[ur]\ar@/d\curv/[rr] && 0 }](/images/math/2/f/c/2fc969ce25938349a6e271c06d55c491.png)
Let's first prove the algebra fact from above: Projecting onto the first factor gives a map of short exact sequences:
![\displaystyle \xymatrix{ \Z \ar[r]^-{(-x,?)} \ar[d]_{x} & \Z \times \Z/a \ar[r] \ar[d]_{\binom 1 0} & \Z/ab \ar[d] \\ \Z \ar[r]_{id} & \Z \ar[r] & 0 }](/images/math/4/7/e/47ef08424ac521a6d9f01e86d4261ddf.png)
The conclusion is then immediate from the snake lemma. The only nontrivial left to prove now is that there is only a single isomorphism class for a diagram of the form
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr] \ar@/u\curv/[rr] & & \Z/28 \\ \Z \ar[ur] \ar[dr] & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur] \ar@/d\curv/[rr] & & \Z/240 }](/images/math/f/6/2/f625357f4e60c4f9e1bf7db191677417.png)
with the obvious exactness properties derived from the braid above. We will convert such a diagram to the one displayed in the braid above in several steps. First, the maps between the 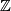 entries are certainly given by multiplication with
entries are certainly given by multiplication with 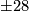 and
and 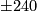 , respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower
, respectively. The isomorphism of braids induced by changing the signs of the upper and/or lower 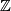 as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps
as necessary converts these into the multiplication with the positive numbers. Since the upper and lower maps 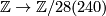 are surjective the isomorphism of braids given by dividing by the image of
are surjective the isomorphism of braids given by dividing by the image of 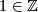 in
in 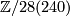 converts these maps into the projections. Switching the sign on the
converts these maps into the projections. Switching the sign on the 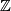 -summand of
-summand of 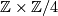 and using the fact from above, we can change the upper map
and using the fact from above, we can change the upper map 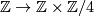 (which is given by
(which is given by 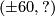 into the
into the 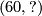 . The lower map will then be determined to be
. The lower map will then be determined to be 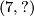 by commutativity of the left square. Our given diagram is thus isomorphic to the following:
by commutativity of the left square. Our given diagram is thus isomorphic to the following:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,?)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,?)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/e/c/1/ec1e69ddaae3d1edc2dfb3236807a7ad.png)
By commutativity of the upper triangle, we also know that the only possibilities for the upper map are 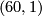 and
and 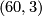 (otherwise the upper map would not be surjective). Multiplying with
(otherwise the upper map would not be surjective). Multiplying with 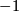 on the
on the 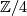 -summand if necessary we can arrange this to be
-summand if necessary we can arrange this to be 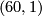 . Now for the fun part: Composing with the shearing isomorphism
. Now for the fun part: Composing with the shearing isomorphism 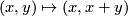 of
of 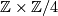 leaves the map
leaves the map 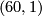 fixed, since
fixed, since 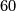 is divisible by
is divisible by 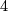 , and changes the map
, and changes the map 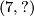 to
to 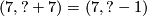 . So using the induced isomorphism of braids we can arrange for
. So using the induced isomorphism of braids we can arrange for 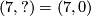 without changing anything fixed before:
without changing anything fixed before:
![\displaystyle \def\curv{1.5pc} \xymatrix{ & \Z \ar[dr]^{(60,1)} \ar@/u\curv/[rr]^{pr} & & \Z/28 \\ \Z \ar[ur]^{28} \ar[dr]_{240} & & \Z \times \Z/4 \ar[ur] \ar[dr] & \\ & \Z \ar[ur]_{(7,0)} \ar@/d\curv/[rr]_{pr} & & \Z/240 }](/images/math/d/6/a/d6af79bd3c2ef4e1b505f85f91436870.png)
The other two maps are now determined: For the lower triangle to commute we must have the lower right map be 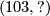 (
(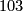 being the multiplicative inverse of
being the multiplicative inverse of 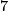 modulo
modulo 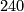 . For the composition with the upper left map to be zero, the second component has to be
. For the composition with the upper left map to be zero, the second component has to be 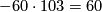 modulo
modulo 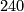 . For other sequence to be exact we need the restriction to
. For other sequence to be exact we need the restriction to 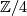 of the unknown map
of the unknown map 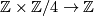 injective (the kernel is torsionfree) so it has to be of the form
injective (the kernel is torsionfree) so it has to be of the form 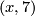 or
or 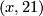 . For the upper triangle to commute one then finds the following congruences modulo
. For the upper triangle to commute one then finds the following congruences modulo  to be solved:
to be solved:
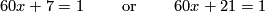
which amounts to finding solutions to
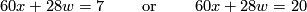
which is obviously impossible in the first case. The solutions modulo  of the second equation are given by
of the second equation are given by 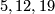 and
and 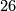 . For the composition with the lower left map to be zero this number has to be divisible by
. For the composition with the lower left map to be zero this number has to be divisible by 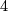 and only
and only 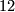 is. This concludes negotiations.
is. This concludes negotiations.