Wu class
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:43, 18 February 2014 and the changes since publication. |
|
The user responsible for this page is Karlheinz Knapp. No other user may edit this page at present. |
Contents |
1 Introduction
The Wu class of a manifold  is a characteristic class allowing a computation of the Stiefel-Whitney classes of
is a characteristic class allowing a computation of the Stiefel-Whitney classes of  by knowing only
by knowing only 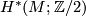 and the action of the Steenrod squares.
and the action of the Steenrod squares.
2 Definition
 be a closed topological
be a closed topological  -manifold,
-manifold, ![[M]\in H_{n}(M;\Zz/2)](/images/math/9/3/4/9345d0a191a038e84bcec9b1764bfe6e.png) its fundamental class,
its fundamental class, 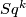 the
the  -th Steenrod square and
-th Steenrod square and 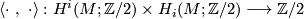
![a\mapsto a\cap \lbrack M]](/images/math/7/c/d/7cdea1ce2260dd4ec586438c1f8e5cd4.png) , induces isomorphisms
, induces isomorphisms
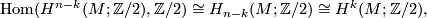
under which the homomorphism ![x\mapsto \left\langle Sq^{k}(x),[M]\right\rangle](/images/math/b/5/c/b5cc737c4817d6fbd30eda5218da8c07.png) from
from 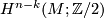 to
to 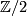 corresponds to a well defined cohomology class
corresponds to a well defined cohomology class 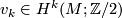 . This cohomology class is called the
. This cohomology class is called the  -th Wu class of
-th Wu class of  ([Milnor&Stasheff1974, §11]). We may rewrite its definition equivalently as an identity
([Milnor&Stasheff1974, §11]). We may rewrite its definition equivalently as an identity
![\left\langle v_{k}\cup x,[M]\right\rangle =\left\langle Sq^{k}(x),[M]\right\rangle \quad \quad \text{ for all }x\in H^{n-k}(M;\Zz/2).](/images/math/8/6/3/863cd20a89c4ac2cd739a96dac9edac2.png)
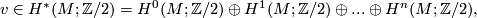
as the formal sum
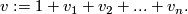
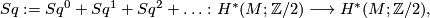
![\left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle \quad \quad \text{for all} x\in H^{\ast }(M;\Zz/2),](/images/math/c/0/e/c0e8ed4066d130b358a5483c4a7e8a98.png)
which may also be used as a definition of the total Wu class of  . From the definition it is clear that the Wu class is defined even for a Poincaré complex
. From the definition it is clear that the Wu class is defined even for a Poincaré complex 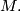
3 Relation to Stiefel-Whitney classes
From now on all manifolds are supposed to be smooth. The following theorem of Wu Wen-Tsun ([Wu1950]) allows a computation of the Stiefel-Whitney classes 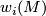 of
of  using only
using only 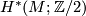 and the action of the Steenrod squares:
and the action of the Steenrod squares:
Theorem 3.1.
The total Stiefel-Whitney class of ,
, 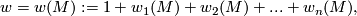
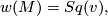
or equivalently
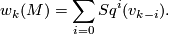
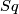 is a ring automorphism of
is a ring automorphism of 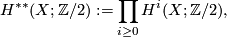
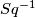 is defined on
is defined on 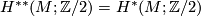 and we may write
and we may write
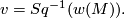
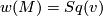 may be used to extend the definition of the Stiefel-Whitney classes to Poincaré complexes.
may be used to extend the definition of the Stiefel-Whitney classes to Poincaré complexes.
4 An example
The following example is taken from [Milnor&Stasheff1974, §11]. If 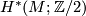 is of the form
is of the form ![\Zz/2[x]/(x^{dm+1}),](/images/math/6/5/c/65c29e0ebee7028abd18cb8bd1b13e90.png) where
where 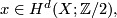
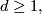
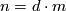 , for example if
, for example if 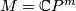 , then
, then
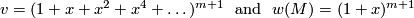
with
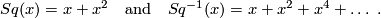
5 A generalization
The following example is taken from [Atiyah&Hirzebruch1961]. Let  be a natural ring automorphism of
be a natural ring automorphism of 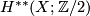 and
and 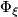 the Thom isomorphism of a real vector bundle
the Thom isomorphism of a real vector bundle  on
on  . Define
. Define
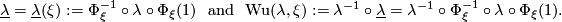
If 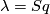 , then
, then 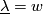 is the total Stiefel-Whitney classes
is the total Stiefel-Whitney classes 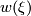 of
of  ([Milnor&Stasheff1974, §8]) and with
([Milnor&Stasheff1974, §8]) and with 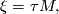 the tangent bundle of
the tangent bundle of 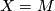 , we have
, we have 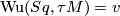 , the total Wu class of
, the total Wu class of  . In general
. In general 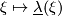 and
and 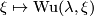 define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula
define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula
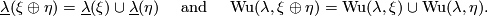
Such a characteristic class is determined by a power series ![f(x) \in \Zz/2[[x]]](/images/math/3/0/0/300a143c4e14656a1e01b918742b48b7.png) , which is given by its value on the universal line bundle. The generalized Wu class
, which is given by its value on the universal line bundle. The generalized Wu class 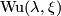 is defined as a commutator class, thus measuring how
is defined as a commutator class, thus measuring how  and
and 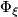 commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in
commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in  -Theory and rational cohomology is formulated. This relation is more than only formal: Let
-Theory and rational cohomology is formulated. This relation is more than only formal: Let 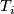 be the
be the  -th Todd polynomial, then
-th Todd polynomial, then 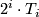 is a rational polynomial with denominators prime to
is a rational polynomial with denominators prime to 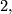 hence its reduction to mod
hence its reduction to mod  cohomology is well defined. Then Atiyah and Hirzebruch proved:
cohomology is well defined. Then Atiyah and Hirzebruch proved:
Theorem 5.1 [Atiyah&Hirzebruch1961].
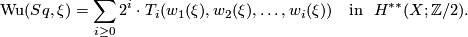
The proof is by comparing the power series belonging to the multiplicative characteristic classes on both sides of the equation, which turn out to be 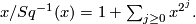 For a continuous map
For a continuous map 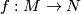 between closed differentiable manifolds the analogue of the Riemann-Roch formula is
between closed differentiable manifolds the analogue of the Riemann-Roch formula is
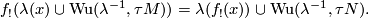
Here 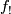 is the Umkehr map of
is the Umkehr map of  defined by
defined by 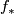 via Poincaré duality. In the case
via Poincaré duality. In the case 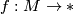 , this reduces to
, this reduces to ![\left\langle \textup{Wu}(\lambda ,\tau M)\cup x,[M]\right\rangle =\left\langle \lambda (x),[M]\right\rangle ,](/images/math/d/8/d/d8d960bd4b12cc779162fbe2c14f2ea5.png) generalizing (2).
generalizing (2).
6 Applications
- The definition of the total Wu class
 and
and 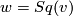 show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type.
show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type.
- Since the Stiefel-Whitney classes of a closed
 -manifold determine its un-oriented bordism class [Thom1954, Théorém IV.10], a corollary of (1) is: Homotopy equivalent manifolds are un-oriented bordant.
-manifold determine its un-oriented bordism class [Thom1954, Théorém IV.10], a corollary of (1) is: Homotopy equivalent manifolds are un-oriented bordant.
- Inserting the Stiefel-Whitney classes of
 for
for  in
in
![\displaystyle \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle,](/images/math/5/c/e/5cea724fb027d95c0a54475900642848.png)
and using
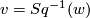 one gets relations between Stiefel-Whitney numbers of
one gets relations between Stiefel-Whitney numbers of  -manifolds. It is a result of Dold ([Dold1956]) that all relations between Stiefel-Whitney numbers of
-manifolds. It is a result of Dold ([Dold1956]) that all relations between Stiefel-Whitney numbers of  -manifolds are obtained in this way.
-manifolds are obtained in this way.
- Conditions on the Wu classes
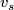 for nonbounding manifolds are given in [Stong&Yoshida1987].
for nonbounding manifolds are given in [Stong&Yoshida1987].
- For an appearance of the Wu class in surgery theory see [Madsen&Milgram1979, Ch. 4].
6.1 Remarks
- Most of the above has analogues for odd primes, e.g. see [Atiyah&Hirzebruch1961].
- Not directly related to the Wu class is Wu's explicit formula for the action of Steenrod squares on the Stiefel-Whitney classes of a vector bundle
 (see [Milnor&Stasheff1974, §8]):
(see [Milnor&Stasheff1974, §8]):
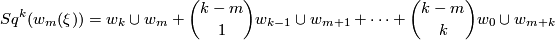
where 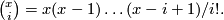
7 References
- [Atiyah&Hirzebruch1961] M. F. Atiyah and F. Hirzebruch, Cohomologie-Operationen und charakteristische Klassen, Math. Z. 77 (1961), 149–187. MR0156361 (27 #6285) Zbl 0109.16002
- [Dold1956] A. Dold, Erzeugende der Thomschen Algebra
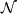 , Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
, Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Stong&Yoshida1987] R. Stong and T. Yoshida, Wu classes, Proc. Amer. Math. Soc. 100 (1987), no.2, 352–354. MR884478 (88e:57025) Zbl 0644.57011
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Wu1950] W. Wu, Classes caractéristiques et
 -carrés d'une variété, C. R. Acad. Sci. Paris, 230 (1950), 508–511. MR0035992 (12,42f) Zbl 0035.11002
-carrés d'une variété, C. R. Acad. Sci. Paris, 230 (1950), 508–511. MR0035992 (12,42f) Zbl 0035.11002
8 External links
- Wu class in nLab
- Wu class in the Wikipedia page on Stiefel-Whitney classes