Wu class
(→Applications) |
m (→Relation to Stiefel-Whitney classes) |
||
| (11 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{Authors|Knapp | + | {{Authors|Karlheinz Knapp}} |
==Introduction== | ==Introduction== | ||
<wikitex>; | <wikitex>; | ||
| Line 7: | Line 7: | ||
<wikitex>; | <wikitex>; | ||
Let $M$ be a closed topological $n$-manifold, $[M]\in H_{n}(M;\Zz/2)$ its fundamental class, $Sq^{k}$ the $k$-th Steenrod square and $$\left\langle \cdot~,~\cdot \right\rangle:H^{i}(M;\Zz/2)\times H_{i}(M;\Zz /2)\longrightarrow \Zz/2$$ the usual Kronecker pairing. This pairing, together with the Poincaré duality isomorphism $a\mapsto a\cap \lbrack M]$, induces isomorphisms | Let $M$ be a closed topological $n$-manifold, $[M]\in H_{n}(M;\Zz/2)$ its fundamental class, $Sq^{k}$ the $k$-th Steenrod square and $$\left\langle \cdot~,~\cdot \right\rangle:H^{i}(M;\Zz/2)\times H_{i}(M;\Zz /2)\longrightarrow \Zz/2$$ the usual Kronecker pairing. This pairing, together with the Poincaré duality isomorphism $a\mapsto a\cap \lbrack M]$, induces isomorphisms | ||
| − | + | $$ \textup{Hom}(H^{n-k}(M;\Zz/2), \Zz/2) \cong H_{n-k}(M;\Zz /2)\cong H^{k}(M;\Zz/2), $$ | |
under which the homomorphism $x\mapsto \left\langle Sq^{k}(x),[M]\right\rangle $ from $H^{n-k}(M;\Zz/2)$ to $\Zz/2$ corresponds to a well defined cohomology class $v_{k}\in H^{k}(M;\Zz/2)$. This cohomology class is called the $k$-th Wu class of $M$ (\cite[§11]{Milnor&Stasheff1974}). We may rewrite its definition equivalently as an identity | under which the homomorphism $x\mapsto \left\langle Sq^{k}(x),[M]\right\rangle $ from $H^{n-k}(M;\Zz/2)$ to $\Zz/2$ corresponds to a well defined cohomology class $v_{k}\in H^{k}(M;\Zz/2)$. This cohomology class is called the $k$-th Wu class of $M$ (\cite[§11]{Milnor&Stasheff1974}). We may rewrite its definition equivalently as an identity | ||
\begin{equation} \label{W1} \left\langle v_{k}\cup x,[M]\right\rangle =\left\langle Sq^{k}(x),[M]\right\rangle \quad \quad \text{ for all }x\in H^{n-k}(M;\Zz/2). | \begin{equation} \label{W1} \left\langle v_{k}\cup x,[M]\right\rangle =\left\langle Sq^{k}(x),[M]\right\rangle \quad \quad \text{ for all }x\in H^{n-k}(M;\Zz/2). | ||
| − | \end{equation} Define the total Wu class $$v\in H^{\ast }(M;\Zz/2)=H^{0}(M;\Zz/2)\oplus H^{1}(M;\Zz /2)\oplus | + | \end{equation} Define the total Wu class $$v\in H^{\ast }(M;\Zz/2)=H^{0}(M;\Zz/2)\oplus H^{1}(M;\Zz /2)\oplus ... \oplus H^{n}(M;\Zz/2),$$ |
as the formal sum | as the formal sum | ||
| − | + | $$ v:=1+v_{1}+v_{2}+...+v_{n}. $$ | |
Using the total Steenrod square, $$Sq:=Sq^{0}+Sq^{1}+Sq^{2}+ \dots \colon H^{\ast}(M;\Zz /2)\longrightarrow H^{\ast }(M;\Zz/2),$$ equation (\ref{W1}) translates into the following formula | Using the total Steenrod square, $$Sq:=Sq^{0}+Sq^{1}+Sq^{2}+ \dots \colon H^{\ast}(M;\Zz /2)\longrightarrow H^{\ast }(M;\Zz/2),$$ equation (\ref{W1}) translates into the following formula | ||
\begin{equation} \label{W2} \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle \quad \quad \text{for all} x\in H^{\ast }(M;\Zz/2), \end{equation} | \begin{equation} \label{W2} \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle \quad \quad \text{for all} x\in H^{\ast }(M;\Zz/2), \end{equation} | ||
| Line 24: | Line 24: | ||
{{beginthm|Theorem|}} | {{beginthm|Theorem|}} | ||
The total Stiefel-Whitney class of $M$, $$w=w(M):=1+w_{1}(M)+w_{2}(M)+...+w_{n}(M),$$ is given by | The total Stiefel-Whitney class of $M$, $$w=w(M):=1+w_{1}(M)+w_{2}(M)+...+w_{n}(M),$$ is given by | ||
| − | + | $$ w(M)=Sq(v), $$ | |
| − | or equivalently | + | or equivalently |
| + | $$ w_{k}(M)=\sum_{i=0}Sq^{i}(v_{k-i}).$$ | ||
{{endthm}} | {{endthm}} | ||
For a proof see \cite[§11]{Milnor&Stasheff1974}. Since $Sq$ is a ring automorphism of $$H^{\ast \ast }(X;\Zz/2):=\prod_{i\geq 0}H^{i}(X;\Zz/2),$$ $Sq^{-1}$ is defined on $H^{\ast \ast }(M;\Zz/2)=H^{\ast }(M;\Zz/2)$ and we may write | For a proof see \cite[§11]{Milnor&Stasheff1974}. Since $Sq$ is a ring automorphism of $$H^{\ast \ast }(X;\Zz/2):=\prod_{i\geq 0}H^{i}(X;\Zz/2),$$ $Sq^{-1}$ is defined on $H^{\ast \ast }(M;\Zz/2)=H^{\ast }(M;\Zz/2)$ and we may write | ||
| − | $$ v=Sq^{-1}(w(M)). $$ The formula $w(M)=Sq(v)$ may be used to extend the definition of the Stiefel-Whitney classes to | + | $$ v=Sq^{-1}(w(M)). $$ The formula $w(M)=Sq(v)$ may be used to extend the definition of the Stiefel-Whitney classes to Poincaré complexes. |
</wikitex> | </wikitex> | ||
| + | |||
==An example== | ==An example== | ||
<wikitex>; | <wikitex>; | ||
The following example is taken from \cite[§11]{Milnor&Stasheff1974}. If $H^{\ast }(M;\Zz/2)$ is of the form $\Zz/2[x]/(x^{dm+1}),$ where $x\in H^{d}(X;\Zz/2),$ $d\geq 1,$ $n=d\cdot m$, for example if $M = \mathbb{C}P^m$, then | The following example is taken from \cite[§11]{Milnor&Stasheff1974}. If $H^{\ast }(M;\Zz/2)$ is of the form $\Zz/2[x]/(x^{dm+1}),$ where $x\in H^{d}(X;\Zz/2),$ $d\geq 1,$ $n=d\cdot m$, for example if $M = \mathbb{C}P^m$, then | ||
| − | + | $$ v=(1+x+x^{2}+x^{4}+\dots)^{m+1}~~\text{and}~~w(M)=(1+x)^{m+1} $$ | |
| − | + | with | |
| + | $$Sq(x)=x+x^{2} \quad \text{and} \quad Sq^{-1}(x)=x+x^{2}+x^{4}+ \dots~.$$ | ||
</wikitex> | </wikitex> | ||
| + | |||
==A generalization== | ==A generalization== | ||
<wikitex>; | <wikitex>; | ||
The following example is taken from {{cite|Atiyah&Hirzebruch1961}}. Let $\lambda $ be a natural ring automorphism of $H^{\ast \ast }(X;\Zz/2)$ and $\Phi _{\xi }$ the Thom isomorphism of a real vector bundle $\xi $ on $X$. Define | The following example is taken from {{cite|Atiyah&Hirzebruch1961}}. Let $\lambda $ be a natural ring automorphism of $H^{\ast \ast }(X;\Zz/2)$ and $\Phi _{\xi }$ the Thom isomorphism of a real vector bundle $\xi $ on $X$. Define | ||
| − | + | $$ \underline{\lambda }=\underline{\lambda }(\xi ):=\Phi _{\xi }^{-1}\circ \lambda \circ \Phi _{\xi }(1)~~\text{and}~~\textup{Wu}(\lambda ,\xi ):=\lambda ^{-1}\circ \underline{\lambda }=\lambda ^{-1}\circ \Phi _{\xi }^{-1}\circ \lambda \circ \Phi _{\xi }(1). $$ | |
| − | + | If $\lambda =Sq$, then $\underline{\lambda }=w$ is the total Stiefel-Whitney classes $w(\xi )$ of $\xi $ (\cite[§8]{Milnor&Stasheff1974}) and with $\xi =\tau M,$ the tangent bundle of $X=M$, we have $\textup{Wu}(Sq,\tau M)=v$, the total Wu class of $M$. In general $\xi \mapsto \underline{\lambda }(\xi )$ and $\xi \mapsto \textup{Wu}(\lambda ,\xi )$ define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula | |
| − | If $\lambda =Sq$, then $\underline{\lambda }=w$ is the total Stiefel-Whitney classes $w(\xi )$ of $\xi $ (\cite[§8]{Milnor&Stasheff1974}) and with $\xi =\tau M,$ the tangent bundle of $X=M$, we have $\textup{Wu}(Sq,\tau M)=v$, the total Wu class of $M$. In general $\xi \mapsto \underline{\lambda }(\xi )$ and $\xi \mapsto \textup{Wu}(\lambda ,\xi )$ define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula | + | $$ \underline{\lambda }(\xi \oplus \eta )=\underline{\lambda }(\xi )\cup \underline{\lambda }(\eta )\quad \text{ and } \quad \textup{Wu}(\lambda ,\xi \oplus \eta )=\textup{Wu}(\lambda ,\xi )\cup \textup{Wu}(\lambda ,\eta ). $$ |
Such a characteristic class is determined by a power series $f(x) \in \Zz/2[[x]]$, which is given by its value on the universal line bundle. The generalized Wu class $\textup{Wu}(\lambda ,\xi )$ is defined as a commutator class, thus measuring how $\lambda $ and $\Phi _{\xi }$ commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in $K$ -Theory and rational cohomology is formulated. This relation is more than only formal: Let $T_{i}$ be the $i$-th Todd polynomial, then $2^{i}\cdot T_{i}$ is a rational polynomial with denominators prime to $2,$ hence its reduction to mod $2$ cohomology is well defined. Then Atiyah and Hirzebruch proved: | Such a characteristic class is determined by a power series $f(x) \in \Zz/2[[x]]$, which is given by its value on the universal line bundle. The generalized Wu class $\textup{Wu}(\lambda ,\xi )$ is defined as a commutator class, thus measuring how $\lambda $ and $\Phi _{\xi }$ commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in $K$ -Theory and rational cohomology is formulated. This relation is more than only formal: Let $T_{i}$ be the $i$-th Todd polynomial, then $2^{i}\cdot T_{i}$ is a rational polynomial with denominators prime to $2,$ hence its reduction to mod $2$ cohomology is well defined. Then Atiyah and Hirzebruch proved: | ||
| − | {{beginthm|Theorem| | + | {{beginthm|Theorem|{{cite|Atiyah&Hirzebruch1961}}}} |
| − | + | $$\textup{Wu}(Sq,\xi )=\sum_{i\geq 0}2^{i}\cdot T_{i}(w_{1}(\xi ),w_{2}(\xi ), \dots ,w_{i}(\xi )) \quad \text{in}~~H^{\ast \ast }(X;\Zz/2). $$ | |
{{endthm}} | {{endthm}} | ||
The proof is by comparing the power series belonging to the multiplicative characteristic classes on both sides of the equation, which turn out to be $ x/Sq^{-1}(x)=1+\sum_{j\geq 0}x^{2^{j}}.$ For a continuous map $f:M\rightarrow N$ between closed differentiable manifolds the analogue of the Riemann-Roch formula is | The proof is by comparing the power series belonging to the multiplicative characteristic classes on both sides of the equation, which turn out to be $ x/Sq^{-1}(x)=1+\sum_{j\geq 0}x^{2^{j}}.$ For a continuous map $f:M\rightarrow N$ between closed differentiable manifolds the analogue of the Riemann-Roch formula is | ||
| − | + | $$ f_{!}(\lambda (x)\cup \textup{Wu}(\lambda ^{-1},\tau M))=\lambda (f_{!}(x))\cup \textup{Wu}(\lambda ^{-1},\tau N). $$ | |
Here $f_{!}$ is the Umkehr map of $f$ defined by $f_{\ast }$ via Poincaré duality. In the case $f:M\rightarrow \ast$, this reduces to $\left\langle \textup{Wu}(\lambda ,\tau M)\cup x,[M]\right\rangle =\left\langle \lambda (x),[M]\right\rangle ,$ generalizing (\ref{W2}). | Here $f_{!}$ is the Umkehr map of $f$ defined by $f_{\ast }$ via Poincaré duality. In the case $f:M\rightarrow \ast$, this reduces to $\left\langle \textup{Wu}(\lambda ,\tau M)\cup x,[M]\right\rangle =\left\langle \lambda (x),[M]\right\rangle ,$ generalizing (\ref{W2}). | ||
</wikitex> | </wikitex> | ||
| + | |||
==Applications== | ==Applications== | ||
<wikitex>; | <wikitex>; | ||
<ol> | <ol> | ||
<li> The definition of the total Wu class $v$ and $w=Sq(v)$ show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type. | <li> The definition of the total Wu class $v$ and $w=Sq(v)$ show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type. | ||
| − | <li> Since the Stiefel-Whitney classes of a closed $n$-manifold determine its un-oriented bordism class \cite[Théorém IV.10]{Thom1954}, a corollary of (1) is: Homotopy equivalent manifolds are | + | <li> Since the Stiefel-Whitney classes of a closed $n$-manifold determine its un-oriented bordism class \cite[Théorém IV.10]{Thom1954}, a corollary of (1) is: Homotopy equivalent manifolds are un-oriented bordant. |
<li> Inserting the Stiefel-Whitney classes of $M$ for $x$ in | <li> Inserting the Stiefel-Whitney classes of $M$ for $x$ in | ||
$$ \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle, $$ | $$ \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle, $$ | ||
and using $v=Sq^{-1}(w)$ one gets relations between Stiefel-Whitney numbers of $n$-manifolds. It is a result of Dold ({{cite|Dold1956}}) that all relations between Stiefel-Whitney numbers of $n$-manifolds are obtained in this way. | and using $v=Sq^{-1}(w)$ one gets relations between Stiefel-Whitney numbers of $n$-manifolds. It is a result of Dold ({{cite|Dold1956}}) that all relations between Stiefel-Whitney numbers of $n$-manifolds are obtained in this way. | ||
| − | <li> Conditions on the Wu classes $v_{s}$ for nonbounding manifolds are given in {{cite|Stong&Yoshida1987}}. | + | <li> Conditions on the Wu classes $v_{s}$ for nonbounding manifolds are given in {{cite|Stong&Yoshida1987}}. |
| + | <li> For an appearance of the Wu class in surgery theory see \cite{Madsen&Milgram1979|Ch. 4}.</ol> | ||
| + | </wikitex> | ||
=== Remarks === | === Remarks === | ||
| + | <wikitex>; | ||
# Most of the above has analogues for odd primes, e.g. see {{cite|Atiyah&Hirzebruch1961}}. | # Most of the above has analogues for odd primes, e.g. see {{cite|Atiyah&Hirzebruch1961}}. | ||
# Not directly related to the Wu class is Wu's explicit formula for the action of Steenrod squares on the Stiefel-Whitney classes of a vector bundle $\xi $ (see \cite[§8]{Milnor&Stasheff1974}): | # Not directly related to the Wu class is Wu's explicit formula for the action of Steenrod squares on the Stiefel-Whitney classes of a vector bundle $\xi $ (see \cite[§8]{Milnor&Stasheff1974}): | ||
| − | + | $$ Sq^{k}(w_{m}(\xi ))=w_{k}\cup w_{m}+\binom{k-m}{1}w_{k-1}\cup w_{m+1}+ \dots + \binom{k-m}{k}w_{0}\cup w_{m+k} $$ | |
| + | where $\binom{x}{i}=x(x-1)\dots(x-i+1)/i!.$ | ||
</wikitex> | </wikitex> | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| + | == External links == | ||
| + | * [http://ncatlab.org/nlab/show/Wu+class Wu class in nLab] | ||
| + | * [[Wikipedia:Stiefel-Whitney_class#Wu_classes|Wu class]] in the Wikipedia page on Stiefel-Whitney classes | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
Latest revision as of 04:11, 3 February 2021
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:43, 18 February 2014 and the changes since publication. |
|
The user responsible for this page is Karlheinz Knapp. No other user may edit this page at present. |
Contents |
1 Introduction
The Wu class of a manifold  is a characteristic class allowing a computation of the Stiefel-Whitney classes of
is a characteristic class allowing a computation of the Stiefel-Whitney classes of  by knowing only
by knowing only 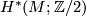 and the action of the Steenrod squares.
and the action of the Steenrod squares.
2 Definition
 be a closed topological
be a closed topological  -manifold,
-manifold, ![[M]\in H_{n}(M;\Zz/2)](/images/math/9/3/4/9345d0a191a038e84bcec9b1764bfe6e.png) its fundamental class,
its fundamental class, 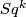 the
the  -th Steenrod square and
-th Steenrod square and 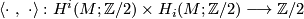
![a\mapsto a\cap \lbrack M]](/images/math/7/c/d/7cdea1ce2260dd4ec586438c1f8e5cd4.png) , induces isomorphisms
, induces isomorphisms
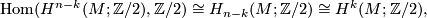
under which the homomorphism ![x\mapsto \left\langle Sq^{k}(x),[M]\right\rangle](/images/math/b/5/c/b5cc737c4817d6fbd30eda5218da8c07.png) from
from 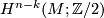 to
to 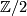 corresponds to a well defined cohomology class
corresponds to a well defined cohomology class 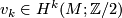 . This cohomology class is called the
. This cohomology class is called the  -th Wu class of
-th Wu class of  ([Milnor&Stasheff1974, §11]). We may rewrite its definition equivalently as an identity
([Milnor&Stasheff1974, §11]). We may rewrite its definition equivalently as an identity
![\left\langle v_{k}\cup x,[M]\right\rangle =\left\langle Sq^{k}(x),[M]\right\rangle \quad \quad \text{ for all }x\in H^{n-k}(M;\Zz/2).](/images/math/8/6/3/863cd20a89c4ac2cd739a96dac9edac2.png)
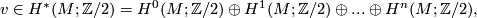
as the formal sum
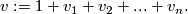
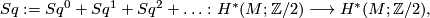
![\left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle \quad \quad \text{for all} x\in H^{\ast }(M;\Zz/2),](/images/math/c/0/e/c0e8ed4066d130b358a5483c4a7e8a98.png)
which may also be used as a definition of the total Wu class of  . From the definition it is clear that the Wu class is defined even for a Poincaré complex
. From the definition it is clear that the Wu class is defined even for a Poincaré complex 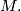
3 Relation to Stiefel-Whitney classes
From now on all manifolds are supposed to be smooth. The following theorem of Wu Wen-Tsun ([Wu1950]) allows a computation of the Stiefel-Whitney classes 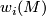 of
of  using only
using only 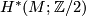 and the action of the Steenrod squares:
and the action of the Steenrod squares:
Theorem 3.1.
The total Stiefel-Whitney class of ,
, 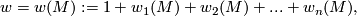
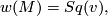
or equivalently
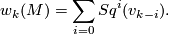
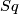 is a ring automorphism of
is a ring automorphism of 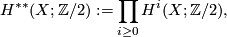
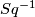 is defined on
is defined on 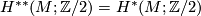 and we may write
and we may write
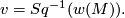
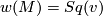 may be used to extend the definition of the Stiefel-Whitney classes to Poincaré complexes.
may be used to extend the definition of the Stiefel-Whitney classes to Poincaré complexes.
4 An example
The following example is taken from [Milnor&Stasheff1974, §11]. If 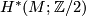 is of the form
is of the form ![\Zz/2[x]/(x^{dm+1}),](/images/math/6/5/c/65c29e0ebee7028abd18cb8bd1b13e90.png) where
where 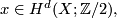
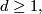
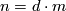 , for example if
, for example if 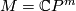 , then
, then
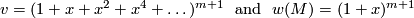
with
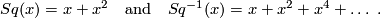
5 A generalization
The following example is taken from [Atiyah&Hirzebruch1961]. Let  be a natural ring automorphism of
be a natural ring automorphism of 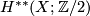 and
and 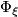 the Thom isomorphism of a real vector bundle
the Thom isomorphism of a real vector bundle  on
on  . Define
. Define
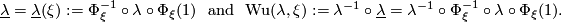
If 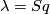 , then
, then 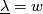 is the total Stiefel-Whitney classes
is the total Stiefel-Whitney classes 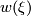 of
of  ([Milnor&Stasheff1974, §8]) and with
([Milnor&Stasheff1974, §8]) and with 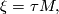 the tangent bundle of
the tangent bundle of 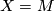 , we have
, we have 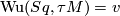 , the total Wu class of
, the total Wu class of  . In general
. In general 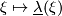 and
and 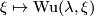 define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula
define multiplicative characteristic classes, translating Whitney sum into cup product, i.e. they satisfy a Whitney product type formula
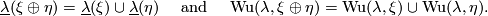
Such a characteristic class is determined by a power series ![f(x) \in \Zz/2[[x]]](/images/math/3/0/0/300a143c4e14656a1e01b918742b48b7.png) , which is given by its value on the universal line bundle. The generalized Wu class
, which is given by its value on the universal line bundle. The generalized Wu class 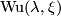 is defined as a commutator class, thus measuring how
is defined as a commutator class, thus measuring how  and
and 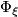 commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in
commute. This is similar to the situation considered in the (differential) Riemann-Roch formulas, in which the interaction between the Chern character and the Thom isomorphism in  -Theory and rational cohomology is formulated. This relation is more than only formal: Let
-Theory and rational cohomology is formulated. This relation is more than only formal: Let 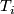 be the
be the  -th Todd polynomial, then
-th Todd polynomial, then 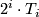 is a rational polynomial with denominators prime to
is a rational polynomial with denominators prime to 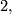 hence its reduction to mod
hence its reduction to mod  cohomology is well defined. Then Atiyah and Hirzebruch proved:
cohomology is well defined. Then Atiyah and Hirzebruch proved:
Theorem 5.1 [Atiyah&Hirzebruch1961].
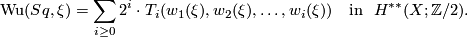
The proof is by comparing the power series belonging to the multiplicative characteristic classes on both sides of the equation, which turn out to be 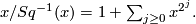 For a continuous map
For a continuous map 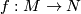 between closed differentiable manifolds the analogue of the Riemann-Roch formula is
between closed differentiable manifolds the analogue of the Riemann-Roch formula is
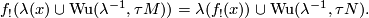
Here 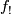 is the Umkehr map of
is the Umkehr map of  defined by
defined by 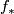 via Poincaré duality. In the case
via Poincaré duality. In the case 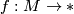 , this reduces to
, this reduces to ![\left\langle \textup{Wu}(\lambda ,\tau M)\cup x,[M]\right\rangle =\left\langle \lambda (x),[M]\right\rangle ,](/images/math/d/8/d/d8d960bd4b12cc779162fbe2c14f2ea5.png) generalizing (2).
generalizing (2).
6 Applications
- The definition of the total Wu class
 and
and 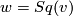 show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type.
show, that the Stiefel-Whitney classes of a smooth manifold are invariants of its homotopy type.
- Since the Stiefel-Whitney classes of a closed
 -manifold determine its un-oriented bordism class [Thom1954, Théorém IV.10], a corollary of (1) is: Homotopy equivalent manifolds are un-oriented bordant.
-manifold determine its un-oriented bordism class [Thom1954, Théorém IV.10], a corollary of (1) is: Homotopy equivalent manifolds are un-oriented bordant.
- Inserting the Stiefel-Whitney classes of
 for
for  in
in
![\displaystyle \left\langle v\cup x,[M]\right\rangle =\left\langle Sq(x),[M]\right\rangle,](/images/math/5/c/e/5cea724fb027d95c0a54475900642848.png)
and using
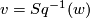 one gets relations between Stiefel-Whitney numbers of
one gets relations between Stiefel-Whitney numbers of  -manifolds. It is a result of Dold ([Dold1956]) that all relations between Stiefel-Whitney numbers of
-manifolds. It is a result of Dold ([Dold1956]) that all relations between Stiefel-Whitney numbers of  -manifolds are obtained in this way.
-manifolds are obtained in this way.
- Conditions on the Wu classes
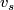 for nonbounding manifolds are given in [Stong&Yoshida1987].
for nonbounding manifolds are given in [Stong&Yoshida1987].
- For an appearance of the Wu class in surgery theory see [Madsen&Milgram1979, Ch. 4].
6.1 Remarks
- Most of the above has analogues for odd primes, e.g. see [Atiyah&Hirzebruch1961].
- Not directly related to the Wu class is Wu's explicit formula for the action of Steenrod squares on the Stiefel-Whitney classes of a vector bundle
 (see [Milnor&Stasheff1974, §8]):
(see [Milnor&Stasheff1974, §8]):
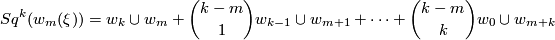
where 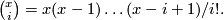
7 References
- [Atiyah&Hirzebruch1961] M. F. Atiyah and F. Hirzebruch, Cohomologie-Operationen und charakteristische Klassen, Math. Z. 77 (1961), 149–187. MR0156361 (27 #6285) Zbl 0109.16002
- [Dold1956] A. Dold, Erzeugende der Thomschen Algebra
 , Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
, Math. Z. 65 (1956), 25–35. MR0079269 (18,60c) Zbl 0071.17601
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Stong&Yoshida1987] R. Stong and T. Yoshida, Wu classes, Proc. Amer. Math. Soc. 100 (1987), no.2, 352–354. MR884478 (88e:57025) Zbl 0644.57011
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Wu1950] W. Wu, Classes caractéristiques et
 -carrés d'une variété, C. R. Acad. Sci. Paris, 230 (1950), 508–511. MR0035992 (12,42f) Zbl 0035.11002
-carrés d'une variété, C. R. Acad. Sci. Paris, 230 (1950), 508–511. MR0035992 (12,42f) Zbl 0035.11002
8 External links
- Wu class in nLab
- Wu class in the Wikipedia page on Stiefel-Whitney classes