Whitehead torsion (Ex)
From Manifold Atlas
Revision as of 20:38, 28 August 2013 by Diarmuid Crowley (Talk | contribs)
Show that ![1 - t - t^{-1} \in \Zz[\Zz/5]](/images/math/2/8/5/28577726cd93bb2c4c5750b1686c1454.png) for
for 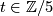 the generator is a unit and hence
defines an element
the generator is a unit and hence
defines an element 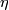 in
in 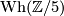 . Prove that we obtain a well-defined map
. Prove that we obtain a well-defined map
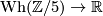
by sending the class represented by the ![\Zz[\Zz/5]](/images/math/c/4/7/c47437a1f5e6e690b9e440d2eaac1f1a.png) -automorphism
-automorphism ![f \colon \Zz[\Zz/5]^n \to \Zz[\Zz/5]^n](/images/math/a/a/4/aa45aa847ac82be4bf86bead28b0d0af.png) to
to  , where
, where 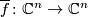 is the
is the 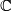 -linear map
-linear map
![\displaystyle f \otimes_{\Zz[\Zz/5]} \id_{\Cc} \colon \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc \to \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc](/images/math/2/1/5/215a48a8f87766a233c0ac9407a69cc7.png)
with respect to the 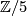 -action on
-action on 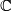 given by multiplication with
given by multiplication with 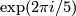 .
Finally show that
.
Finally show that 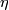 generates an infinite cyclic subgroup in
generates an infinite cyclic subgroup in 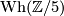 .
.
This is a detailed version of [Milnor1966, Example 6.6] and [Kreck&Lück2005, Ex 5.4].
- t - t^{-1} \in \Zz[\Zz/5]$ for $t\in \Zz/5$ the generator is a unit and hence defines an element $\eta$ in $\textup{Wh}(\Zz/5)$. Prove that we obtain a well-defined map $$\textup{Wh}(\Zz/5) \to \Rr$$ by sending the class represented by the $\Zz[\Zz/5]$-automorphism $f \colon \Zz[\Zz/5]^n \to \Zz[\Zz/5]^n$ to $\ln(|\det(\overline{f})|)$, where $\overline{f} \colon \Cc^n \to \Cc^n$ is the $\Cc$-linear map $$f \otimes_{\Zz[\Zz/5]} \id_{\Cc} \colon \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc \to \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc$$ with respect to the $\Zz/5$-action on $\Cc$ given by multiplication with $\exp(2 \pi i/5)$. Finally show that $\eta$ generates an infinite cyclic subgroup in $\textup{Wh}(\Zz/5)$. This is a detailed version of {{citeD|Milnor1966|Example 6.6}} and {{citeD|Kreck&Lück2005|Ex 5.4}}. [[Category:Exercises]] [[Category:Exercises with solution]]1 - t - t^{-1} \in \Zz[\Zz/5] for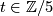 the generator is a unit and hence
defines an element
the generator is a unit and hence
defines an element 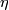 in
in 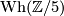 . Prove that we obtain a well-defined map
. Prove that we obtain a well-defined map
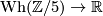
by sending the class represented by the ![\Zz[\Zz/5]](/images/math/c/4/7/c47437a1f5e6e690b9e440d2eaac1f1a.png) -automorphism
-automorphism ![f \colon \Zz[\Zz/5]^n \to \Zz[\Zz/5]^n](/images/math/a/a/4/aa45aa847ac82be4bf86bead28b0d0af.png) to
to  , where
, where 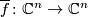 is the
is the 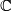 -linear map
-linear map
![\displaystyle f \otimes_{\Zz[\Zz/5]} \id_{\Cc} \colon \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc \to \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc](/images/math/2/1/5/215a48a8f87766a233c0ac9407a69cc7.png)
with respect to the 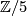 -action on
-action on 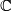 given by multiplication with
given by multiplication with 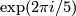 .
Finally show that
.
Finally show that 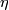 generates an infinite cyclic subgroup in
generates an infinite cyclic subgroup in 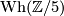 .
.
This is a detailed version of [Milnor1966, Example 6.6] and [Kreck&Lück2005, Ex 5.4].