Talk:Structure set (Ex)
(Difference between revisions)
m |
Marek Kaluba (Talk | contribs) m (typos) |
||
| Line 2: | Line 2: | ||
'''Solution''': | '''Solution''': | ||
| − | We begin with the map | + | We begin with the map $\mathcal{S}^s(M) \to \mathcal{M}(M)$, from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things: |
* If manifolds $N$ and $N'$ simply homotopy equivalent to $M$ are diffeomorphic then their images by the map belong to the same orbit of $\mathcal{E}^s(M)$-action on $\mathcal{S}^s(M)$. | * If manifolds $N$ and $N'$ simply homotopy equivalent to $M$ are diffeomorphic then their images by the map belong to the same orbit of $\mathcal{E}^s(M)$-action on $\mathcal{S}^s(M)$. | ||
| − | * If two elements of $\mathcal{S}^s(M)$ belong to the same orbit of $\mathcal{E}^s(M)$-action, then | + | * If two elements of $\mathcal{S}^s(M)$ belong to the same orbit of $\mathcal{E}^s(M)$-action, then they are diffeomorphic. |
| − | Let $N$ be a smooth manifold and $f\colon N\to M$ a simple homotopy equivalence. Consider a map which takes $N$ to $[(N,f)]\in \mathcal{S}^ | + | Let $N$ be a smooth manifold and $f\colon N\to M$ a simple homotopy equivalence. Consider a map which takes $N$ to $[(N,f)]\in \mathcal{S}^s(M)$. Suppose now that $N'$ is a manifold diffeomorphic to $N$, and $f'\colon N'\to M$ a simple homotopy equivalence (possibly $N'=N$ and $f\nsim f'$). Then there exists $h\colon M\to M$ such that the following diagram commutes. |
$$ | $$ | ||
Revision as of 08:57, 28 August 2013
Solution:
We begin with the map 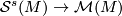 , from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things:
, from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things:
- If manifolds
 and
and 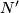 simply homotopy equivalent to
simply homotopy equivalent to Tex syntax error
are diffeomorphic then their images by the map belong to the same orbit of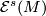 -action on
-action on 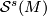 .
.
- If two elements of
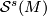 belong to the same orbit of
belong to the same orbit of 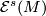 -action, then they are diffeomorphic.
-action, then they are diffeomorphic.
Let  be a smooth manifold and
be a smooth manifold and 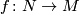 a simple homotopy equivalence. Consider a map which takes
a simple homotopy equivalence. Consider a map which takes  to
to ![[(N,f)]\in \mathcal{S}^s(M)](/images/math/a/0/b/a0bd066d1820ebb79b7b293cf08cf6f5.png) . Suppose now that
. Suppose now that 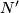 is a manifold diffeomorphic to
is a manifold diffeomorphic to  , and
, and 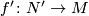 a simple homotopy equivalence (possibly
a simple homotopy equivalence (possibly 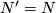 and
and 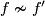 ). Then there exists
). Then there exists 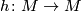 such that the following diagram commutes.
such that the following diagram commutes.
![\displaystyle \xymatrix{ N \ar[r]^{f} \ar[d]^d_{\cong} & M \ar@{.>}[d]^{h}\\ N'\ar[r]^{f'}& M }](/images/math/c/4/a/c4abb3f8f8e0ec1ca20372334218c540.png)
Map  is given by composition
is given by composition 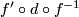 (the homotopy inverse) and hence is a simple homotopy equivalence. The commutativity of the diagram tells us that in
(the homotopy inverse) and hence is a simple homotopy equivalence. The commutativity of the diagram tells us that in 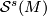 we have the following equalities.
we have the following equalities.
![\displaystyle h\cdot [(N,f)] = [(N,h\circ f)]=[(N,f'\circ d\circ f^{-1}\circ f\simeq f'\circ d)]=[(N',f')],](/images/math/4/7/9/4791859a73cb925e3025f03a13999be4.png)
where  denotes the
denotes the 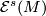 -action. Therefore
-action. Therefore ![[(N,f)]](/images/math/b/b/5/bb5ef132530c2698542a58ecd8d89515.png) and
and ![[(N',f')]](/images/math/8/5/8/858d6cb132fbf93242faa0a054ae7fe8.png) belong to the same orbit.
belong to the same orbit.
![[(N,f)],[(N',f')]\in \mathcal{S}^s(M)](/images/math/1/7/f/17fd2cca910495263b3a5e1d86fdaafc.png) belong to the same orbit of
belong to the same orbit of 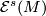 -action. It means, that there exist a simple homotopy equivalence
-action. It means, that there exist a simple homotopy equivalence 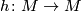 such that
such that ![\displaystyle h\cdot[(N,f)]=[(N,h\circ f)]=[(N',f')].](/images/math/4/a/7/4a7f9c7103b48031968606c3d570ecf6.png)
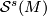 is just the existence of a diffeomorphism
is just the existence of a diffeomorphism 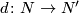 making the following diagram commute.
making the following diagram commute.
![\displaystyle \xymatrix{ N \ar[r]^{f} \ar@{.>}[d]^d & M \ar[d]^{h}\\ N'\ar[r]^{f'}& M } .](/images/math/d/f/2/df2c7efd93154406ec2ffbb64d0929f1.png)