Talk:Structure set (Ex)
(Difference between revisions)
m |
Marek Kaluba (Talk | contribs) m (typos) |
||
| Line 2: | Line 2: | ||
'''Solution''': | '''Solution''': | ||
| − | We begin with the map | + | We begin with the map $\mathcal{S}^s(M) \to \mathcal{M}(M)$, from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things: |
* If manifolds $N$ and $N'$ simply homotopy equivalent to $M$ are diffeomorphic then their images by the map belong to the same orbit of $\mathcal{E}^s(M)$-action on $\mathcal{S}^s(M)$. | * If manifolds $N$ and $N'$ simply homotopy equivalent to $M$ are diffeomorphic then their images by the map belong to the same orbit of $\mathcal{E}^s(M)$-action on $\mathcal{S}^s(M)$. | ||
| − | * If two elements of $\mathcal{S}^s(M)$ belong to the same orbit of $\mathcal{E}^s(M)$-action, then | + | * If two elements of $\mathcal{S}^s(M)$ belong to the same orbit of $\mathcal{E}^s(M)$-action, then they are diffeomorphic. |
| − | Let $N$ be a smooth manifold and $f\colon N\to M$ a simple homotopy equivalence. Consider a map which takes $N$ to $[(N,f)]\in \mathcal{S}^ | + | Let $N$ be a smooth manifold and $f\colon N\to M$ a simple homotopy equivalence. Consider a map which takes $N$ to $[(N,f)]\in \mathcal{S}^s(M)$. Suppose now that $N'$ is a manifold diffeomorphic to $N$, and $f'\colon N'\to M$ a simple homotopy equivalence (possibly $N'=N$ and $f\nsim f'$). Then there exists $h\colon M\to M$ such that the following diagram commutes. |
$$ | $$ | ||
Revision as of 08:57, 28 August 2013
Solution:
We begin with the map 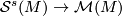 , from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things:
, from the simple structure set of manifolds simply homotopy equivalent to the orbit space and then we show two things:
- If manifolds
 and
and 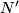 simply homotopy equivalent to
simply homotopy equivalent to  are diffeomorphic then their images by the map belong to the same orbit of
are diffeomorphic then their images by the map belong to the same orbit of 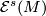 -action on
-action on 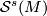 .
.
- If two elements of
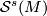 belong to the same orbit of
belong to the same orbit of 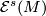 -action, then they are diffeomorphic.
-action, then they are diffeomorphic.
Let  be a smooth manifold and
be a smooth manifold and 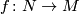 a simple homotopy equivalence. Consider a map which takes
a simple homotopy equivalence. Consider a map which takes  to
to ![[(N,f)]\in \mathcal{S}^s(M)](/images/math/a/0/b/a0bd066d1820ebb79b7b293cf08cf6f5.png) . Suppose now that
. Suppose now that 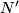 is a manifold diffeomorphic to
is a manifold diffeomorphic to  , and
, and 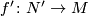 a simple homotopy equivalence (possibly
a simple homotopy equivalence (possibly 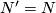 and
and 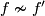 ). Then there exists
). Then there exists 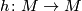 such that the following diagram commutes.
such that the following diagram commutes.
![\displaystyle \xymatrix{ N \ar[r]^{f} \ar[d]^d_{\cong} & M \ar@{.>}[d]^{h}\\ N'\ar[r]^{f'}& M }](/images/math/c/4/a/c4abb3f8f8e0ec1ca20372334218c540.png)
Map  is given by composition
is given by composition 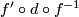 (the homotopy inverse) and hence is a simple homotopy equivalence. The commutativity of the diagram tells us that in
(the homotopy inverse) and hence is a simple homotopy equivalence. The commutativity of the diagram tells us that in 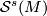 we have the following equalities.
we have the following equalities.
![\displaystyle h\cdot [(N,f)] = [(N,h\circ f)]=[(N,f'\circ d\circ f^{-1}\circ f\simeq f'\circ d)]=[(N',f')],](/images/math/4/7/9/4791859a73cb925e3025f03a13999be4.png)
where  denotes the
denotes the 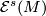 -action. Therefore
-action. Therefore ![[(N,f)]](/images/math/b/b/5/bb5ef132530c2698542a58ecd8d89515.png) and
and ![[(N',f')]](/images/math/8/5/8/858d6cb132fbf93242faa0a054ae7fe8.png) belong to the same orbit.
belong to the same orbit.
![[(N,f)],[(N',f')]\in \mathcal{S}^s(M)](/images/math/1/7/f/17fd2cca910495263b3a5e1d86fdaafc.png) belong to the same orbit of
belong to the same orbit of 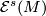 -action. It means, that there exist a simple homotopy equivalence
-action. It means, that there exist a simple homotopy equivalence 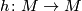 such that
such that ![\displaystyle h\cdot[(N,f)]=[(N,h\circ f)]=[(N',f')].](/images/math/4/a/7/4a7f9c7103b48031968606c3d570ecf6.png)
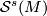 is just the existence of a diffeomorphism
is just the existence of a diffeomorphism 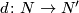 making the following diagram commute.
making the following diagram commute.
![\displaystyle \xymatrix{ N \ar[r]^{f} \ar@{.>}[d]^d & M \ar[d]^{h}\\ N'\ar[r]^{f'}& M } .](/images/math/d/f/2/df2c7efd93154406ec2ffbb64d0929f1.png)