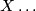Talk:S-duality I (Ex)
Exercise 0.1 (first part).
Any finite CW complex  has an
has an 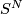 -dual, for
-dual, for  sufficiently large.
sufficiently large.
Proof.
(tentative: see remarks below)
Let  be a finite pointed CW complex with basepoint
be a finite pointed CW complex with basepoint 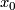 . Embed
. Embed 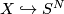 with regular neighbourhood
with regular neighbourhood  , so that
, so that
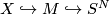
with 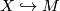 a homotopy-equivalence and
a homotopy-equivalence and  an
an  -dimensional manifold-with-boundary embedded in
-dimensional manifold-with-boundary embedded in 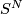 .
.
Now let
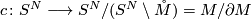
be the collapse map,
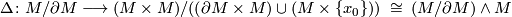
be the map induced by
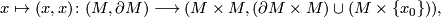
and let  be the composite
be the composite
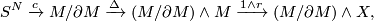
where 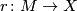 is a chosen homotopy-inverse for
is a chosen homotopy-inverse for 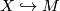 .
.
The map  is degree-1 by construction, so
is degree-1 by construction, so ![c_*([S^N]) = [M] \in \widetilde{H}_N(M / \partial M) = H_N(M,\partial M)](/images/math/0/2/b/02b7da8222f37956580221cf5573d189.png) .
.
For any 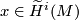 , we have the identity
, we have the identity
![\displaystyle x\setminus \Delta_*([M]) \;=\; x\cap [M] \;\in\; \widetilde{H}_{N-i}(M / \partial M) = H_{N-i}(M,\partial M),](/images/math/c/a/8/ca8536778122062ab9650f9fbf0ef619.png)
so by Poincare-Lefschetz duality,
![\displaystyle -\setminus (\Delta\circ c)_*([S^N]) \;\colon\; \widetilde{H}^i(M) \longrightarrow \widetilde{H}_{N-i}(M / \partial M)](/images/math/2/2/2/222aac0c05c6a48069391f72af49c324.png)
is an isomorphism for all  .
.
In general for any 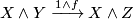 and
and 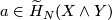 ,
,
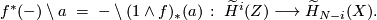
So in our case we have
![\displaystyle -\setminus \alpha_*([S^N]) \;=\; r^*(-)\setminus (\Delta\circ c)_*([S^N]) \;\colon\; \widetilde{H}^i(X) \longrightarrow \widetilde{H}_{N-i}(M / \partial M)](/images/math/7/9/7/7979bae793d7ee1b17a139357f70fdba.png)
which is an isomorphism by above and the fact that  is a homotopy-equivalence. This witnesses that
is a homotopy-equivalence. This witnesses that 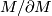 is an
is an 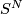 -dual of
-dual of  .
.

Remark 0.2.
This uses reduced homology instead of unreduced homology in the definition of  -duality, which is correct (?) as we are using smash products rather than direct products.
-duality, which is correct (?) as we are using smash products rather than direct products.
Remark 0.3.
It doesn't seem to be immediately clear why the map  defined above is the correct geometric `diagonal' map to use so that the claimed identity
defined above is the correct geometric `diagonal' map to use so that the claimed identity 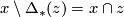 holds. It seems more natural to use the map
holds. It seems more natural to use the map
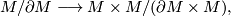
but this would witness that 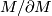 is an
is an 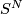 -dual of
-dual of 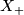 , rather than
, rather than