Talk:Microbundles (Ex)
From Manifold Atlas
Revision as of 19:11, 29 May 2012 by Marek Kaluba (Talk | contribs)
Let us begin with the definition of microbundle.
Definition 0.1.
An -dimensional microbundle is a quadruple
-dimensional microbundle is a quadruple 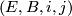 such that there is a sequence
such that there is a sequence 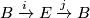
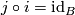
- for all
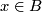 there exist open neigbourhood
there exist open neigbourhood  and an open neighbourhood
and an open neighbourhood  of
of 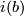 and a homeomorphism
and a homeomorphism