Talk:Microbundles (Ex)
Marek Kaluba (Talk | contribs) |
Marek Kaluba (Talk | contribs) (2nd exercise WIP) |
||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | + | In case of daubts You should get familiar with the definition of [[Microbundle|microbundle]]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{beginthm|Exercise|{{citeD|Milnor1964|Lemma 2.1}}}} | {{beginthm|Exercise|{{citeD|Milnor1964|Lemma 2.1}}}} | ||
| Line 24: | Line 11: | ||
To prove that the second condition is satisfied we need to use local chart around $x$. | To prove that the second condition is satisfied we need to use local chart around $x$. | ||
Choose $U$ to be one of the open sets coming from atlas of $M$ and let $\phi\colon U\to \mathbb{R}^n$ be associated chart. The obvious choice for neighbourhood $V\subset M\times M$ is to take $U\times U$. The first naive candidate for $h\colon V=U\times U\to U\times\mathbb{R}^n$ would be map $\id\times \phi$. However such $h$ fails to make the following diagram commute | Choose $U$ to be one of the open sets coming from atlas of $M$ and let $\phi\colon U\to \mathbb{R}^n$ be associated chart. The obvious choice for neighbourhood $V\subset M\times M$ is to take $U\times U$. The first naive candidate for $h\colon V=U\times U\to U\times\mathbb{R}^n$ would be map $\id\times \phi$. However such $h$ fails to make the following diagram commute | ||
| + | |||
$$ | $$ | ||
\xymatrix{ | \xymatrix{ | ||
| − | U \ar[ | + | &U\times U\ar[rd]^{p_1}\ar[dd]^h&\\ |
| − | + | U\ar[ru]^{\Delta_M}\ar[rd]_{\id\times\{0\}} & & U\\ | |
| + | &U\times \Rr^n\ar[ru]_{p_1}&} | ||
$$ | $$ | ||
since $(u,u)$ is mapped to $(u,\phi(u))$ and $\phi(u)$ doesn't necessarily be $0$ (well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment: $h(u,v)=(u,h(u)-h(v))$. | since $(u,u)$ is mapped to $(u,\phi(u))$ and $\phi(u)$ doesn't necessarily be $0$ (well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment: $h(u,v)=(u,h(u)-h(v))$. | ||
| Line 39: | Line 28: | ||
We have two concurring definitions of micro-tangent bundle. The first is given by the exercise above, the second by forgeting about the vector bundle structure on $TM$ and treating it just as a microbundle $(TM, M, \pi,s_0)$ where $M\xrightarrow{s_0} TM$ is the zero section. | We have two concurring definitions of micro-tangent bundle. The first is given by the exercise above, the second by forgeting about the vector bundle structure on $TM$ and treating it just as a microbundle $(TM, M, \pi,s_0)$ where $M\xrightarrow{s_0} TM$ is the zero section. | ||
| − | + | To fix the notation please consult the definition of microbundle isomorphism on page on [[Microbundle|microbundles]] . | |
| − | + | In our case we have | |
| − | + | ||
$$ | $$ | ||
\xymatrix{ | \xymatrix{ | ||
| − | + | & V\ar[dd]^H \ar[rd]^{p_1}&\\ | |
| − | + | M\ar[dr]_{\Delta_M}\ar[ur]^{s_0} & & M\\ | |
| + | & M\times M \ar[ru]&} | ||
$$ | $$ | ||
| − | |||
| − | + | where $V\subset TM$ is an open neighbourhood of the zero section. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | where $V\subset TM$ is an open neighbourhood of the zero section | + | |
{{endproof}} | {{endproof}} | ||
| + | We need to find a map $H\colon V\to | ||
</wikitex> | </wikitex> | ||
Revision as of 02:10, 30 May 2012
In case of daubts You should get familiar with the definition of microbundle.
Exercise 0.1 [Milnor1964, Lemma 2.1].
Let  be a topological manifold. Show that
be a topological manifold. Show that 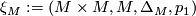 is a microbundle.
is a microbundle.
Proof.
Let  be a topological manifold. Then the composition
be a topological manifold. Then the composition 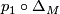 sends
sends 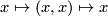 , so the first condition in the definition is satisfied.
, so the first condition in the definition is satisfied.
To prove that the second condition is satisfied we need to use local chart around  .
Choose
.
Choose  to be one of the open sets coming from atlas of
to be one of the open sets coming from atlas of  and let
and let 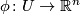 be associated chart. The obvious choice for neighbourhood
be associated chart. The obvious choice for neighbourhood 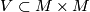 is to take
is to take 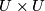 . The first naive candidate for
. The first naive candidate for 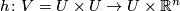 would be map
would be map 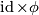 . However such
. However such  fails to make the following diagram commute
fails to make the following diagram commute
![\displaystyle \xymatrix{ &U\times U\ar[rd]^{p_1}\ar[dd]^h&\\ U\ar[ru]^{\Delta_M}\ar[rd]_{\id\times\{0\}} & & U\\ &U\times \Rr^n\ar[ru]_{p_1}&}](/images/math/4/c/d/4cd938113e2094115097195f965b3b01.png)
since 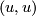 is mapped to
is mapped to 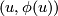 and
and 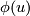 doesn't necessarily be
doesn't necessarily be  (well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment:
(well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment: 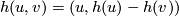 .
.

Exercise 0.2 [Milnor1964, Theorem 2.2].
Let  be a (paracompact!) smooth manifold. Show that
be a (paracompact!) smooth manifold. Show that  and
and 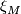 are isomorphic microbundles.
are isomorphic microbundles.
Proof.
We have two concurring definitions of micro-tangent bundle. The first is given by the exercise above, the second by forgeting about the vector bundle structure on  and treating it just as a microbundle
and treating it just as a microbundle 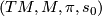 where
where 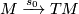 is the zero section.
is the zero section.
To fix the notation please consult the definition of microbundle isomorphism on page on microbundles .
In our case we have
![\displaystyle \xymatrix{ & V\ar[dd]^H \ar[rd]^{p_1}&\\ M\ar[dr]_{\Delta_M}\ar[ur]^{s_0} & & M\\ & M\times M \ar[ru]&}](/images/math/6/3/f/63f5d1fba623e066d09038da1d7fa1f8.png)
where 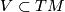 is an open neighbourhood of the zero section.
is an open neighbourhood of the zero section.

We need to find a map $H\colon V\to
$ (well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment: $h(u,v)=(u,h(u)-h(v))$. {{endproof}} {{beginthm|Exercise|{{citeD|Milnor1964|Theorem 2.2}}}} Let $M$ be a (paracompact!) smooth manifold. Show that $TM$ and $\xi_M$ are isomorphic microbundles. {{endthm}} {{beginproof}} We have two concurring definitions of micro-tangent bundle. The first is given by the exercise above, the second by forgeting about the vector bundle structure on $TM$ and treating it just as a microbundle $(TM, M, \pi,s_0)$ where $M\xrightarrow{s_0} TM$ is the zero section. To fix the notation please consult the definition of microbundle isomorphism on page on [[Microbundle|microbundles]] . In our case we have $$ \xymatrix{ & V\ar[dd]^H \ar[rd]^{p_1}&\ M\ar[dr]_{\Delta_M}\ar[ur]^{s_0} & & M\ & M\times M \ar[ru]&} $$ where $V\subset TM$ is an open neighbourhood of the zero section. {{endproof}} We need to find a map $H\colon V\to M be a topological manifold. Show that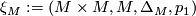 is a microbundle.
is a microbundle.
Proof.
Let  be a topological manifold. Then the composition
be a topological manifold. Then the composition 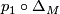 sends
sends 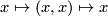 , so the first condition in the definition is satisfied.
, so the first condition in the definition is satisfied.
To prove that the second condition is satisfied we need to use local chart around  .
Choose
.
Choose  to be one of the open sets coming from atlas of
to be one of the open sets coming from atlas of  and let
and let 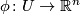 be associated chart. The obvious choice for neighbourhood
be associated chart. The obvious choice for neighbourhood 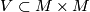 is to take
is to take 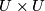 . The first naive candidate for
. The first naive candidate for 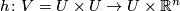 would be map
would be map 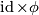 . However such
. However such  fails to make the following diagram commute
fails to make the following diagram commute
![\displaystyle \xymatrix{ &U\times U\ar[rd]^{p_1}\ar[dd]^h&\\ U\ar[ru]^{\Delta_M}\ar[rd]_{\id\times\{0\}} & & U\\ &U\times \Rr^n\ar[ru]_{p_1}&}](/images/math/4/c/d/4cd938113e2094115097195f965b3b01.png)
since 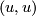 is mapped to
is mapped to 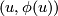 and
and 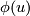 doesn't necessarily be
doesn't necessarily be  (well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment:
(well, it depends on our definition of an atlas of a manifold?). We need just a small adjustment: 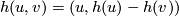 .
.

Exercise 0.2 [Milnor1964, Theorem 2.2].
Let  be a (paracompact!) smooth manifold. Show that
be a (paracompact!) smooth manifold. Show that  and
and 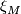 are isomorphic microbundles.
are isomorphic microbundles.
Proof.
We have two concurring definitions of micro-tangent bundle. The first is given by the exercise above, the second by forgeting about the vector bundle structure on  and treating it just as a microbundle
and treating it just as a microbundle 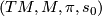 where
where 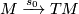 is the zero section.
is the zero section.
To fix the notation please consult the definition of microbundle isomorphism on page on microbundles .
In our case we have
![\displaystyle \xymatrix{ & V\ar[dd]^H \ar[rd]^{p_1}&\\ M\ar[dr]_{\Delta_M}\ar[ur]^{s_0} & & M\\ & M\times M \ar[ru]&}](/images/math/6/3/f/63f5d1fba623e066d09038da1d7fa1f8.png)
where 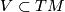 is an open neighbourhood of the zero section.
is an open neighbourhood of the zero section.

We need to find a map $H\colon V\to