Talk:Microbundles (Ex)
(Difference between revisions)
Marek Kaluba (Talk | contribs) |
|||
| Line 3: | Line 3: | ||
{{beginthm|Definition|}} | {{beginthm|Definition|}} | ||
An $n$-dimensional microbundle is a quadruple $(E,B,i,j)$ such that there is a sequence $$B\xrightarrow{i} E\xrightarrow{j} B$$ and the following conditions hold. | An $n$-dimensional microbundle is a quadruple $(E,B,i,j)$ such that there is a sequence $$B\xrightarrow{i} E\xrightarrow{j} B$$ and the following conditions hold. | ||
| − | + | #$j\circ i=\id_B$ | |
| − | + | #for all $x\in B$ there exist open neigbourhood $U\subset B$ and an open neighbourhood $V\subset E$ of $i(b)$ and a homeomorphism $$h\colon V\to U\times \mathbb{R}^n.$$ | |
| + | |||
| + | Moreover, the homeomorphism above must make the following diagram commute: | ||
{{endthm}} | {{endthm}} | ||
| + | {{beginthm|Exercise|{{citeD|Milnor1964|Lemma 2.1, Theorem 2.2}}}} | ||
| + | Let $M$ be a topological manifold. Show that $\xi_M : = (M \times M, M, \Delta_M, p_1)$ is a microbundle. | ||
| + | {{endthm}} | ||
| + | Let $M$ be a topological manifold. Then the composition $p_1\circ\Delta_M$ sends $x\mapsto (x,x)\mapsto x$, so the first condition in the definition is satisfied. | ||
| + | To prove that the second condition is satisfied we need to use local chart around $x$. | ||
| + | Choose $U$ to be one of the open sets coming from atlas of $M$ and let $\phi\colon U\to \mathbb{R}^n$ be associated chart. The obvious candidate for $V\subset M\times M$ is to take $U\times U$. Now the first naive candidate for $h\colon V=U\timesU\to U\times\mathbb{R}^n$ would be map $\id\times \phi$. However | ||
| + | |||
| + | {{beginthm|Exercise|{{citeD|Milnor1964|Lemma 2.1, Theorem 2.2}}}} | ||
| + | Let $M$ be a smooth manifold. Show that $TM$ and $\xi_M$ are isomorphic microbundles. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 19:25, 29 May 2012
Let us begin with the definition of microbundle.
Definition 0.1.
An -dimensional microbundle is a quadruple
-dimensional microbundle is a quadruple 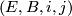 such that there is a sequence
such that there is a sequence 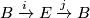
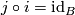
- for all
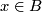 there exist open neigbourhood
there exist open neigbourhood  and an open neighbourhood
and an open neighbourhood  of
of 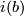 and a homeomorphism
and a homeomorphism 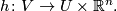
Moreover, the homeomorphism above must make the following diagram commute:
Exercise 0.2 [Milnor1964, Lemma 2.1, Theorem 2.2].
Let  be a topological manifold. Show that
be a topological manifold. Show that 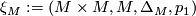 is a microbundle.
is a microbundle.
Let  be a topological manifold. Then the composition
be a topological manifold. Then the composition 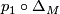 sends
sends 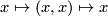 , so the first condition in the definition is satisfied.
, so the first condition in the definition is satisfied.
To prove that the second condition is satisfied we need to use local chart around  .
.
 to be one of the open sets coming from atlas of
to be one of the open sets coming from atlas of  and let
and let 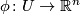 be associated chart. The obvious candidate for
be associated chart. The obvious candidate for 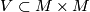 is to take
is to take 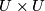 . Now the first naive candidate for
. Now the first naive candidate for Tex syntax errorwould be map
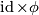 . However
. However
Exercise 0.3 [Milnor1964, Lemma 2.1, Theorem 2.2].
Let  be a smooth manifold. Show that
be a smooth manifold. Show that  and
and 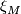 are isomorphic microbundles.
are isomorphic microbundles.