Talk:Fibre homotopy trivial bundles (Ex)
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
We consider 5-dimensional real vector bundles over $S^4$. | We consider 5-dimensional real vector bundles over $S^4$. | ||
| − | Isomorphism classes of these are given by their clutching function in $\pi_3(O_5)$ | + | Isomorphism classes of these are given by their clutching function in $\pi_3(O_5)$. |
| + | |||
Given that $J:\pi_3(O_5)\to \pi_3(G_5)$ is isomorphic to the surjection $\mathbb Z\to \mathbb Z/24$, | Given that $J:\pi_3(O_5)\to \pi_3(G_5)$ is isomorphic to the surjection $\mathbb Z\to \mathbb Z/24$, | ||
we see that the vector bundle $\xi_k$ corresponding to $24k$ times the generator | we see that the vector bundle $\xi_k$ corresponding to $24k$ times the generator | ||
has a sphere bundle $\pi:S(\xi_k)\to S^4$ which is fiber homotopically trivial, so in particular we have | has a sphere bundle $\pi:S(\xi_k)\to S^4$ which is fiber homotopically trivial, so in particular we have | ||
homotopy equivalences $f_k:S(\xi_k)\to S^4\times S^4$. | homotopy equivalences $f_k:S(\xi_k)\to S^4\times S^4$. | ||
| − | From another exercise we know that stably $TS(\xi_k)\cong \pi^*\xi_k$. From a third exercise we know that | + | |
| − | the first Pontryagin class of $xi_k$ is $48k$. It follows that the first Pontryagin class of $S(\xi_k)$ | + | From another exercise we know that stably $TS(\xi_k)\cong \pi^*\xi_k$. |
| − | is non-trivial, since under $f_k$ the map $pi$ just corresponds to projection to one factor. | + | From a third exercise we know that the first Pontryagin class of $\xi_k$ is $48k$. |
| + | |||
| + | It follows that the first Pontryagin class of $S(\xi_k)$ | ||
| + | is non-trivial, since under $f_k$ the map $\pi$ just corresponds to projection to one factor. | ||
Hence $f_k$ is a homotopy equivalence which doesn't preserve the first Pontryagin class, as $S^4\times S^4$ has | Hence $f_k$ is a homotopy equivalence which doesn't preserve the first Pontryagin class, as $S^4\times S^4$ has | ||
stably trivial tangent bundle, hence trivial $p_1$. | stably trivial tangent bundle, hence trivial $p_1$. | ||
| − | Similarly one can argue with $(4n+1)$-dimensional vector bundles over $S^{4n}$; the J-homomorphism has always | + | Similarly one can argue with $(4n+1)$-dimensional vector bundles over $S^{4n}$; the $J$-homomorphism has always |
a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces | a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces | ||
homotopy equivalences $S(\xi_k)\to S^{4n}\times S^{4n}$ which do not preserve $p_n$. | homotopy equivalences $S(\xi_k)\to S^{4n}\times S^{4n}$ which do not preserve $p_n$. | ||
</wikitex> | </wikitex> | ||
Revision as of 20:17, 29 May 2012
We consider 5-dimensional real vector bundles over 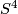 .
Isomorphism classes of these are given by their clutching function in
.
Isomorphism classes of these are given by their clutching function in 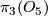 .
.
Given that 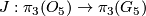 is isomorphic to the surjection
is isomorphic to the surjection 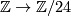 ,
we see that the vector bundle
,
we see that the vector bundle 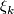 corresponding to
corresponding to 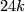 times the generator
has a sphere bundle
times the generator
has a sphere bundle 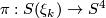 which is fiber homotopically trivial, so in particular we have
homotopy equivalences
which is fiber homotopically trivial, so in particular we have
homotopy equivalences 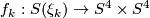 .
.
From another exercise we know that stably 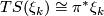 .
From a third exercise we know that the first Pontryagin class of
.
From a third exercise we know that the first Pontryagin class of 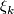 is
is 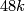 .
.
It follows that the first Pontryagin class of 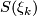 is non-trivial, since under
is non-trivial, since under 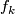 the map
the map  just corresponds to projection to one factor.
Hence
just corresponds to projection to one factor.
Hence 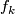 is a homotopy equivalence which doesn't preserve the first Pontryagin class, as
is a homotopy equivalence which doesn't preserve the first Pontryagin class, as 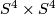 has
stably trivial tangent bundle, hence trivial
has
stably trivial tangent bundle, hence trivial 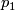 .
.
Similarly one can argue with 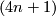 -dimensional vector bundles over
-dimensional vector bundles over 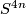 ; the
; the 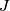 -homomorphism has always
a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces
homotopy equivalences
-homomorphism has always
a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces
homotopy equivalences 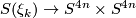 which do not preserve
which do not preserve 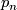 .
.