Talk:Chain duality V (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; This is immediate from the definition that $T_{M,N}(\phi:TM\to N)=e_M\circ T(\phi)$. </wikitex>") |
|||
| Line 2: | Line 2: | ||
This is immediate from the definition that $T_{M,N}(\phi:TM\to N)=e_M\circ T(\phi)$. | This is immediate from the definition that $T_{M,N}(\phi:TM\to N)=e_M\circ T(\phi)$. | ||
</wikitex> | </wikitex> | ||
| + | |||
| + | |||
| + | Somewhat more elaborate, so that we really can see what's going on: | ||
| + | We turn the question around and show that <wikitex>$T_{M,TM}^{-1}(e_M)=\text{id}$.</wikitex> We will suppress all decorations <wikitex>$\Aa$</wikitex> occuring in tensor products and Hom-sets and look at a sequence of maps <wikitex>$$TM\otimes M = \text{Hom}(T^2M,M) \to T^2M\otimes TM = \text{Hom}(T^3M,TM)\to M\otimes TM = \text{Hom}(TM,TM),$$</wikitex> given by <wikitex>$$\phi\mapsto T(\phi) \mapsto (e_{T(M)}\circ T)(\phi).$$</wikitex> This sequence of maps is precisely the previously mentioned <wikitex>$T_{M,TM}^{-1}$</wikitex>. (which has hopefully been treated in the solution to exercise 10 on L-groups) Applying this map to <wikitex>$e_M$</wikitex>, we get <wikitex>$(e_{T(M)}\circ T)(e_M)$</wikitex>, which is equal to the identity map, as part of its very definition. | ||
Latest revision as of 18:05, 29 August 2013
This is immediate from the definition that 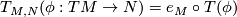 .
.
Somewhat more elaborate, so that we really can see what's going on:
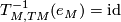 . We will suppress all decorations
. We will suppress all decorations 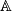 occuring in tensor products and Hom-sets and look at a sequence of maps
occuring in tensor products and Hom-sets and look at a sequence of maps 
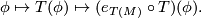
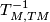 . (which has hopefully been treated in the solution to exercise 10 on L-groups) Applying this map to
. (which has hopefully been treated in the solution to exercise 10 on L-groups) Applying this map to 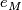 , we get
, we get 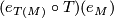 , which is equal to the identity map, as part of its very definition.
, which is equal to the identity map, as part of its very definition.