Talk:Chain duality III (Ex)
(Difference between revisions)
| Line 5: | Line 5: | ||
We have to check the equality of | We have to check the equality of | ||
| − | $T'_{F(M),F(M)}(F (\varphi) \circ G(M))=e'_{F(M)}\circ T'G(M) \circ T'F(\varphi)$ | + | $$T'_{F(M),F(M)}(F (\varphi) \circ G(M))=e'_{F(M)}\circ T'G(M) \circ T'F(\varphi)$$ |
| − | and $F(T_{M,M}\varphi)\circ G(M)=F(e_M)\circ FT\varphi\circ G(M)$. | + | and $$F(T_{M,M}\varphi)\circ G(M)=F(e_M)\circ FT\varphi\circ G(M).$$ |
| + | |||
| + | This follows from the commutative diagram | ||
| + | $$\xymatrix{ | ||
| + | T'F(M)\ar[r]^{T'F(\varphi)} \ar[d]_{G(M)} & | ||
| + | T'FT(M) \ar[r]^{T'G(M)} \ar[d]_{G(TM)} & | ||
| + | T'^2F(M) \ar[d]_{e'_{F(M)}}\\ | ||
| + | FT(M)\ar[r]^{FT\varphi} & | ||
| + | FT^2M\ar[r]^{Fe_M}& | ||
| + | F(M) | ||
| + | }.$$ | ||
</wikitex> | </wikitex> | ||
Revision as of 12:32, 1 June 2012
We check this for objects 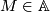 .
.
Let 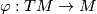 be an element of
be an element of 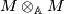 .
.
We have to check the equality of
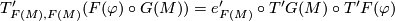
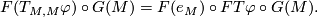
This follows from the commutative diagram
![\displaystyle \xymatrix{ T'F(M)\ar[r]^{T'F(\varphi)} \ar[d]_{G(M)} & T'FT(M) \ar[r]^{T'G(M)} \ar[d]_{G(TM)} & T'^2F(M) \ar[d]_{e'_{F(M)}}\\ FT(M)\ar[r]^{FT\varphi} & FT^2M\ar[r]^{Fe_M}& F(M) }.](/images/math/6/4/5/6456274e424e6bb7d23c6e4c2509b61c.png)