Talk:Chain duality III (Ex)
(Difference between revisions)
(Created page with "We check this for objects in $\mathbb A$. Let $\phi:TM\to M$ be an element of $M\otimes_{\mathbb A}M$. Then $T_{M,M}\phi=(e_M\circ T\phi: TM\to T^2M\to M$.") |
|||
| Line 1: | Line 1: | ||
| + | <wikitex>; | ||
We check this for objects in $\mathbb A$. | We check this for objects in $\mathbb A$. | ||
Let $\phi:TM\to M$ be an element of $M\otimes_{\mathbb A}M$. | Let $\phi:TM\to M$ be an element of $M\otimes_{\mathbb A}M$. | ||
Then $T_{M,M}\phi=(e_M\circ T\phi: TM\to T^2M\to M$. | Then $T_{M,M}\phi=(e_M\circ T\phi: TM\to T^2M\to M$. | ||
| + | </wikitex> | ||
Revision as of 12:14, 1 June 2012
We check this for objects in 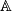 .
.
Let 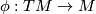 be an element of
be an element of 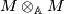 .
Then
.
Then 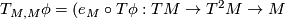 .
.