Talk:5-manifolds: 1-connected/1st edition
From Manifold Atlas
< Talk:5-manifolds: 1-connected(Difference between revisions)
| Line 1: | Line 1: | ||
| − | + | == Conjecture about mapping class groups of 1-connected 5-manifolds == | |
| + | <wikitex>; | ||
| + | Let $M$ be a closed, smooth, 1-connected 5-manifold, [[User:Matthias Kreck|Matthias Kreck]] and [[User:Diarmuid Crowley|Diarmuid Crowley]] conjecture that there is an isomorphism of abelian groups | ||
| + | $$ \pi_0(\SDiff(M)) \cong \Omega_6(B_2(M)) $$ | ||
| + | where $B_2(M)$ is the normal $2$-type of $M$ as defined in {{cite|Kreck1999}}. For example, if $M$ is Spinable with $H_2(M) \cong H$ then | ||
| + | $$ \Omega_6(B_2(M)) \cong \Omega_6^{Spin}(K(H, 2)).$$ | ||
| + | At present we are checking the details of the proof of this conjecture using the methods of {{cite|Kreck1999}}. | ||
| + | </wikitex> | ||
| + | |||
| + | [[User:Diarmuid Crowley|Diarmuid Crowley]] 10:02, 29 September 2009 (UTC) | ||
Latest revision as of 11:59, 17 August 2010
Conjecture about mapping class groups of 1-connected 5-manifolds
Let  be a closed, smooth, 1-connected 5-manifold, Matthias Kreck and Diarmuid Crowley conjecture that there is an isomorphism of abelian groups
be a closed, smooth, 1-connected 5-manifold, Matthias Kreck and Diarmuid Crowley conjecture that there is an isomorphism of abelian groups
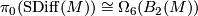
where 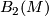 is the normal
is the normal  -type of
-type of  as defined in [Kreck1999]. For example, if
as defined in [Kreck1999]. For example, if  is Spinable with
is Spinable with 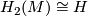 then
then
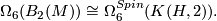
At present we are checking the details of the proof of this conjecture using the methods of [Kreck1999].
Diarmuid Crowley 10:02, 29 September 2009 (UTC)