Talk:5-manifolds: 1-connected
1 Conjecture about mapping class groups of 1-connected 5-manifolds
Let  be a closed, smooth, 1-connected 5-manifold, Matthias Kreck and Diarmuid Crowley conjecture that there is an isomorphism of abelian groups
be a closed, smooth, 1-connected 5-manifold, Matthias Kreck and Diarmuid Crowley conjecture that there is an isomorphism of abelian groups
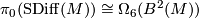
where 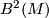 is the normal
is the normal 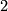 -type of
-type of  as defined in [Kreck1999]. For example, if
as defined in [Kreck1999]. For example, if  is Spinable with
is Spinable with 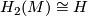 then
then
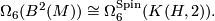
At present we are checking the details of the proof of this conjecture using the methods of [Kreck1999].
Diarmuid Crowley 10:02, 29 September 2009 (UTC)
2 Earlier work of Fang
The group 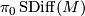 was computed in [Fang1993] provided that
was computed in [Fang1993] provided that 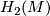 has no
has no 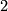 -torsion and no
-torsion and no 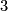 -torsion.
-torsion.
Up-date of conjecture: module structure
If the conjecture above holds, then from the short exact sequence
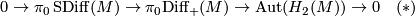
we obtain an action of 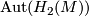 on the abelian group
on the abelian group 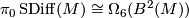 . Diarmuid Crowley and Matthias Kreck also conjecture that the action of
. Diarmuid Crowley and Matthias Kreck also conjecture that the action of 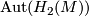 is via the induced action on
is via the induced action on 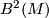 . In particular, if
. In particular, if  is spinable with
is spinable with 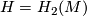 , then
, then 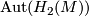 acts on
acts on 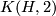 in the obvious way and so on
in the obvious way and so on 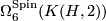 .
.