Symplectic manifolds
m |
|||
| Line 108: | Line 108: | ||
is a symplectic fiber bundle with fiberwise symplectic structure. This construction can be compactified by taking lattices in $G$ which intersect trivially with $K$. A particular example is given by the fiber bundle | is a symplectic fiber bundle with fiberwise symplectic structure. This construction can be compactified by taking lattices in $G$ which intersect trivially with $K$. A particular example is given by the fiber bundle | ||
$$SO(2n)/U(n)\rightarrow SO(2n,p)/U(n)\times SO(p)\rightarrow SO(2n,p)/SO(2n)\times SO(p),$$ | $$SO(2n)/U(n)\rightarrow SO(2n,p)/U(n)\times SO(p)\rightarrow SO(2n,p)/SO(2n)\times SO(p),$$ | ||
| − | and its compactification by lattices.<wikitex> | + | and its compactification by lattices.</wikitex> |
===Symplectic reduction=== | ===Symplectic reduction=== | ||
| Line 115: | Line 115: | ||
by $\mu: M\rightarrow\frak{g}^*$ the moment map of this action. Since $G$ acts on the level set | by $\mu: M\rightarrow\frak{g}^*$ the moment map of this action. Since $G$ acts on the level set | ||
$\mu^{-1}(a),a\in\frak{g}^*$, one can consider the orbit space $\mu^{-1}(a)/G$. It is an orbifold in general, but it happens to be a manifold, when $G$ acts freely on the preimage, and $a$ is a regular point. In this case, $\tilde M=\mu^{-1}(a)/G$ is a symplectic manifold as well, called '''symplectic reduction'''. It is often denoted by $M//G$. | $\mu^{-1}(a),a\in\frak{g}^*$, one can consider the orbit space $\mu^{-1}(a)/G$. It is an orbifold in general, but it happens to be a manifold, when $G$ acts freely on the preimage, and $a$ is a regular point. In this case, $\tilde M=\mu^{-1}(a)/G$ is a symplectic manifold as well, called '''symplectic reduction'''. It is often denoted by $M//G$. | ||
| − | <wikitex> | + | </wikitex> |
===Symplectic cut=== | ===Symplectic cut=== | ||
<wikitex>; | <wikitex>; | ||
Let $(M,\omega)$ be a symplectic manifold with a hamiltonian action of the circle $S^1.$ If $\mu:\rightarrow \mathbb R$ is the moment map, $M_a=\mu^{-1}(a)$ is a regular level, then the action restricted to $M_a$ has no fixed points, hence $M_a$ is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs. | Let $(M,\omega)$ be a symplectic manifold with a hamiltonian action of the circle $S^1.$ If $\mu:\rightarrow \mathbb R$ is the moment map, $M_a=\mu^{-1}(a)$ is a regular level, then the action restricted to $M_a$ has no fixed points, hence $M_a$ is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs. | ||
| − | <wikitex> | + | </wikitex> |
===Coadjoint orbits=== | ===Coadjoint orbits=== | ||
| Line 132: | Line 132: | ||
Consider two symplectic manifolds $(M_1,\omega_1),(M_2,\omega_2)$ of equal dimension and suppose that there are codimension two symplectic submanifolds $V_1\subset M_1,V_2\subset M_2$ and a symplectomorphism $f:V_1\rightarrow V_2$ such that Chern classes of normal bundles satisfy $f^*c_1(\nu_2)=-c_1(\nu_1).$ | Consider two symplectic manifolds $(M_1,\omega_1),(M_2,\omega_2)$ of equal dimension and suppose that there are codimension two symplectic submanifolds $V_1\subset M_1,V_2\subset M_2$ and a symplectomorphism $f:V_1\rightarrow V_2$ such that Chern classes of normal bundles satisfy $f^*c_1(\nu_2)=-c_1(\nu_1).$ | ||
Then by removing tubular neighborhods of $V_1$ and $V_2$ we get manifolds with boundaries. The map $f$ induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with | Then by removing tubular neighborhods of $V_1$ and $V_2$ we get manifolds with boundaries. The map $f$ induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with | ||
| − | $\omega_1$ and $\omega_2$ outside of a tubular neigborhood of the trace of glueing {{cite|Gompf1995}}. The same works if $V_1,V_2$ are symplectic submanifolds of a connected symplectic manifold. <wikitex> | + | $\omega_1$ and $\omega_2$ outside of a tubular neigborhood of the trace of glueing {{cite|Gompf1995}}. The same works if $V_1,V_2$ are symplectic submanifolds of a connected symplectic manifold. </wikitex> |
===Symplectic blow-up=== | ===Symplectic blow-up=== | ||
Revision as of 18:10, 27 November 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
A symplectic manifold is a smooth manifold  together with a differential two-form
together with a differential two-form  that is nondegenerate and closed. The form
that is nondegenerate and closed. The form  is called a symplectic form. The nondegeneracy means that the highest nonzero power of
is called a symplectic form. The nondegeneracy means that the highest nonzero power of  is a volume form on
is a volume form on 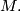 It follows that a symplectic manifold is even dimensional.
It follows that a symplectic manifold is even dimensional.
Symplectic manifolds originated from classical mechanics. The phase space of a dynamical system is the cotangent bundle of the configuration space and it is equipped with a symplectic form. This symplectic form is preserved by the flow of the system.
2 Examples
 The most basic example of a symplectic manifold is
The most basic example of a symplectic manifold is 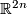 equipped with the form
equipped with the form
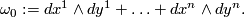
A theorem of Darboux [McDuff&Salamon1998] states that locally every
symplectic manifold if of this form. More precisely, if 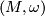 is a symplectic
is a symplectic  -manifold
then for every point
-manifold
then for every point 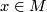 there exists an open neighbourhood
there exists an open neighbourhood 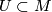 of
of  and a
diffeomorphism
and a
diffeomorphism 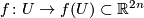 such that the restriction of
such that the restriction of  to
to  is equal to the pull-back
is equal to the pull-back 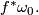 This implies that symplectic manifolds have
no local invariants.
This implies that symplectic manifolds have
no local invariants.
 An area form on an oriented surface is symplectic.
An area form on an oriented surface is symplectic.
 Let
Let  be a smooth manifold and let
be a smooth manifold and let  be a one-form on the cotangent bundle
be a one-form on the cotangent bundle 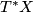 defined as follows.
If
defined as follows.
If  is a vector tangent to
is a vector tangent to 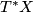 at a point
at a point  then
then 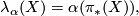 where
where
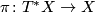 is the projection. In local coordinates the form
is the projection. In local coordinates the form  can be expressed as
can be expressed as
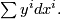 The differential
The differential 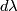 is a symplectic form on the cotangent bundle
is a symplectic form on the cotangent bundle 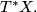
 If
If 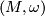 is a closed, i.e. compact and without boundary, symplectic
is a closed, i.e. compact and without boundary, symplectic  -manifold then the cohomology classes
-manifold then the cohomology classes
![[\omega]^k](/images/math/e/6/e/e6eff0918969467a4c56a4750f24fd36.png) are non-zero for
are non-zero for 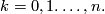 This follows from the fact that the cohomology class of the volume
form
This follows from the fact that the cohomology class of the volume
form 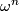 is nonzero on a closed manifold. This necessary condition implies that spheres of dimension greater than
two are not symplectic. More generally, no closed manifold of the form
is nonzero on a closed manifold. This necessary condition implies that spheres of dimension greater than
two are not symplectic. More generally, no closed manifold of the form 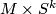 is symplectic for
is symplectic for 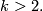
 The complex projective space
The complex projective space 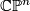 is symplectic with respect to its K\"ahler form.
Its pull back to a complex projective smooth manifold
is symplectic with respect to its K\"ahler form.
Its pull back to a complex projective smooth manifold 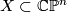 is also symplectic.
More generally, every K\"ahler manifold is symplectic.
is also symplectic.
More generally, every K\"ahler manifold is symplectic.
3 Symmetries
A diffeomorphism 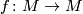 of a symplectic manifold
of a symplectic manifold 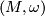 is called symplectic if it preserves
the symplectic form,
is called symplectic if it preserves
the symplectic form, 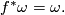 Sometimes such a diffeomorphism is called a symplectiomorphism.
The group of all symplectic diffeomorphisms of
Sometimes such a diffeomorphism is called a symplectiomorphism.
The group of all symplectic diffeomorphisms of 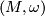 is denoted by
is denoted by
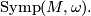
It follows from the nondegeneracy of the symplectic form  the map
the map 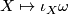 defines an isomorphism
between the vector fields and the one-forms on a symplectic manifold
defines an isomorphism
between the vector fields and the one-forms on a symplectic manifold 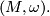 If the flow of a vector field
If the flow of a vector field  preserves the symplectic form we have that
preserves the symplectic form we have that 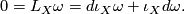 Then the closedness
of the symplectic form implies that the one-form
Then the closedness
of the symplectic form implies that the one-form 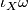 is closed. It follows that the Lie algebra of
the group of symplectic diffeomorhism consists of the vector fields
is closed. It follows that the Lie algebra of
the group of symplectic diffeomorhism consists of the vector fields  for which the one-form
for which the one-form 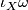 is closed. Hence it can be identified with the space of closed one-forms.
is closed. Hence it can be identified with the space of closed one-forms.
If the one-form 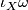 is exact, i.e.
is exact, i.e. 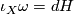 for some function
for some function 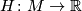 then the vector field
then the vector field  is called Hamiltonian. Symplectic diffeomorphism generated by Hamiltonian flows form
a group
is called Hamiltonian. Symplectic diffeomorphism generated by Hamiltonian flows form
a group 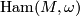 called the group of Hamiltonian diffeomorphism. Its Lie algebra can be
identified with the quotient of the space of smooth functions on
called the group of Hamiltonian diffeomorphism. Its Lie algebra can be
identified with the quotient of the space of smooth functions on  by the constants.
by the constants.
4 Constructions
4.1 Products
The product of symplectic manifolds 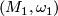 and
and 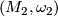 is a symplectic manifold with
respect to the form
is a symplectic manifold with
respect to the form 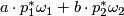 for nonzero real numbers
for nonzero real numbers
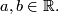 Here
Here 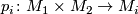 is the projection.
is the projection.
4.2 Bundles
A locally trivial bundle 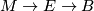 is called symplectic (resp. Hamiltonian) if its structure
group is a subgroup of the group of symplectic (resp. Hamiltonian) diffeomorphisms.
is called symplectic (resp. Hamiltonian) if its structure
group is a subgroup of the group of symplectic (resp. Hamiltonian) diffeomorphisms.
Example. The product of the Hopf bundle with the circle is a symplectic bundle 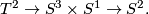 Indeed, the structure group is a group of rotations of the torus and hence it preserves the area.
As we have seen above the product
Indeed, the structure group is a group of rotations of the torus and hence it preserves the area.
As we have seen above the product 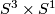 does not admit a symplectic form. This example
shows that, in general, the total space of a symplectic bundle is not symplectic.
does not admit a symplectic form. This example
shows that, in general, the total space of a symplectic bundle is not symplectic.
Let 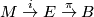 is a compact symplectic bundle over a symplectic base.
According to a theorem of Thurston, if there exists a cohomology class
is a compact symplectic bundle over a symplectic base.
According to a theorem of Thurston, if there exists a cohomology class 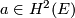 such that
its pull back to every fibre is equal to the class of the symplectic form of the fibre
then there exists a representative
such that
its pull back to every fibre is equal to the class of the symplectic form of the fibre
then there exists a representative  of the class
of the class  such that
such that
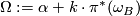 is a symplectic form on
is a symplectic form on  for every big enough
for every big enough 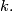
A symplectic fiber bundle may have a symplectic form on the total space which restricts symplectically to the fibers, even if the base is not symplectic. Such bundles are constructed using fat connections. Let there be given a principal fiber bundle
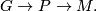
Let 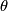 be a connection form,
be a connection form, 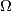 the curvature form of this connection, and
the curvature form of this connection, and 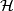 be the horizontal distribution. A vector
be the horizontal distribution. A vector 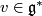 is called fat (with respect to the given connection), if the 2-form
is called fat (with respect to the given connection), if the 2-form
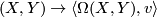
is nondegenerate on the horizontal distribution of the connection. The following theorem yields a construction of a symplectic form on the total space of fiber bundles associated with principal bundles equipped with particular connections.
Theorem 3.1. Let there be given a symplectic manifold 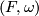 endowed with a hamiltonian action of a Lie group
endowed with a hamiltonian action of a Lie group  . Let
. Let 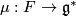 be the moment map of the
be the moment map of the  -action. If
-action. If 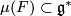 consists of fat vectors, then the associated bundle
consists of fat vectors, then the associated bundle
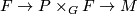
admits a fiberwise symplectic form on the total space.
using this theorem, one can construct examples of symplectic fiber bundles with fiberwise symplectic form on the total space (see examples below).
Example (twistor bundles)
Consider the principal bundle of the orthogonal frame bundles over  -dimensional manifold
-dimensional manifold  :
:
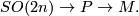
Let 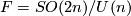 . The associated bundle with fiber
. The associated bundle with fiber 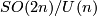 is called the twistor bundle. It is easy to see that
is called the twistor bundle. It is easy to see that 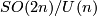 can be identified with a coadjoint orbit
can be identified with a coadjoint orbit 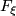 of some
of some 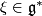 , where
, where 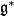 denotes the Lie algebra of
denotes the Lie algebra of 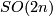 . Moreover, if
. Moreover, if  admits Riemannian metric of pinched curvature with sufficiently small pinching constant then
admits Riemannian metric of pinched curvature with sufficiently small pinching constant then  is fat with respect to the Levi-Civitta connection in the frame bundle. As a result, the whole coadjoint orbit (which is the image of the moment map of the
is fat with respect to the Levi-Civitta connection in the frame bundle. As a result, the whole coadjoint orbit (which is the image of the moment map of the 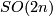 -action) consists of fat vectors. Thus, we obtain a fiberwise symplectic structure on the total space of any twistor bundle
-action) consists of fat vectors. Thus, we obtain a fiberwise symplectic structure on the total space of any twistor bundle
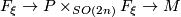
over even-dimensional manifolds of pinched curvature. In particular, twistor bundles over spheres 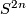 or hyperbolic manifolds, admit fiberwise symplectic structures. The simplest example of this construction is the fibering of
or hyperbolic manifolds, admit fiberwise symplectic structures. The simplest example of this construction is the fibering of 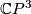 over
over  with fiber
with fiber 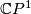 , since it is known that the total space of the twistor bundle over
, since it is known that the total space of the twistor bundle over  is
is 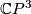 .
.
Example (locally homogeneous complex manifolds)
Let  be a Lie group of non-compact type, which is a real form of a complex Lie group
be a Lie group of non-compact type, which is a real form of a complex Lie group 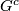 . Choose a parabolic subgroup
. Choose a parabolic subgroup 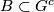 and a maximal compact subgroup
and a maximal compact subgroup  in
in  . Assume that
. Assume that 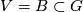 is compact. Then one can show that
is compact. Then one can show that 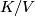 can be identified with a coadjoint orbit of some vector in
can be identified with a coadjoint orbit of some vector in 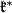 , which is fat with respect to a
, which is fat with respect to a  -invariant connection in the principal bundle
-invariant connection in the principal bundle
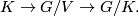
It follows that the associated bundle
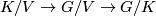
is a symplectic fiber bundle with fiberwise symplectic structure. This construction can be compactified by taking lattices in  which intersect trivially with
which intersect trivially with  . A particular example is given by the fiber bundle
. A particular example is given by the fiber bundle
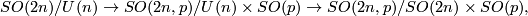
and its compactification by lattices.
4.3 Symplectic reduction
Let  be a Lie group acting on a symplectic manifold
be a Lie group acting on a symplectic manifold 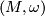 in a hamiltonian way. Denote
by
in a hamiltonian way. Denote
by 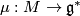 the moment map of this action. Since
the moment map of this action. Since  acts on the level set
acts on the level set
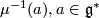 , one can consider the orbit space
, one can consider the orbit space 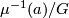 . It is an orbifold in general, but it happens to be a manifold, when
. It is an orbifold in general, but it happens to be a manifold, when  acts freely on the preimage, and
acts freely on the preimage, and  is a regular point. In this case,
is a regular point. In this case, 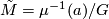 is a symplectic manifold as well, called symplectic reduction. It is often denoted by
is a symplectic manifold as well, called symplectic reduction. It is often denoted by 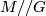 .
.
4.4 Symplectic cut
Let 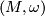 be a symplectic manifold with a hamiltonian action of the circle
be a symplectic manifold with a hamiltonian action of the circle 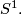 If
If 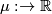 is the moment map,
is the moment map, 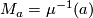 is a regular level, then the action restricted to
is a regular level, then the action restricted to 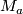 has no fixed points, hence
has no fixed points, hence 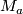 is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs.
is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs.
4.5 Coadjoint orbits
4.6 Symplectic homogeneous spaces
Nilmanifolds, solvmanifolds, homogeneous spaces of semisimple Lie groups
4.7 Donaldson's theorem on submanifolds
4.8 Surgery in codimension 2
Consider two symplectic manifolds 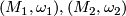 of equal dimension and suppose that there are codimension two symplectic submanifolds
of equal dimension and suppose that there are codimension two symplectic submanifolds 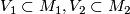 and a symplectomorphism
and a symplectomorphism 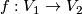 such that Chern classes of normal bundles satisfy
such that Chern classes of normal bundles satisfy 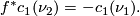 Then by removing tubular neighborhods of
Then by removing tubular neighborhods of 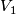 and
and 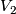 we get manifolds with boundaries. The map
we get manifolds with boundaries. The map  induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with
induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with
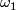 and
and 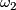 outside of a tubular neigborhood of the trace of glueing [Gompf1995]. The same works if
outside of a tubular neigborhood of the trace of glueing [Gompf1995]. The same works if 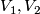 are symplectic submanifolds of a connected symplectic manifold.
are symplectic submanifolds of a connected symplectic manifold.
4.9 Symplectic blow-up
5 Invariants
...
6 Classification/Characterization
...
7 Further discussion
...
8 References
- [Gompf1995] R. E. Gompf, A new construction of symplectic manifolds, Ann. of Math. (2) 142 (1995), no.3, 527–595. MR1356781 (96j:57025) Zbl 0849.53027
- [McDuff&Salamon1998] D. McDuff and D. Salamon, Introduction to symplectic topology, The Clarendon Press Oxford University Press, 1998. MR1698616 (2000g:53098) Zbl 0978.53120
 that is nondegenerate and closed. The form
that is nondegenerate and closed. The form  is called a symplectic form. The nondegeneracy means that the highest nonzero power of
is called a symplectic form. The nondegeneracy means that the highest nonzero power of  is a volume form on
is a volume form on 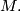 It follows that a symplectic manifold is even dimensional.
It follows that a symplectic manifold is even dimensional.
Symplectic manifolds originated from classical mechanics. The phase space of a dynamical system is the cotangent bundle of the configuration space and it is equipped with a symplectic form. This symplectic form is preserved by the flow of the system.
2 Examples
 The most basic example of a symplectic manifold is
The most basic example of a symplectic manifold is 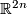 equipped with the form
equipped with the form
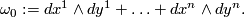
A theorem of Darboux [McDuff&Salamon1998] states that locally every
symplectic manifold if of this form. More precisely, if 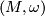 is a symplectic
is a symplectic  -manifold
then for every point
-manifold
then for every point 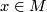 there exists an open neighbourhood
there exists an open neighbourhood 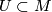 of
of  and a
diffeomorphism
and a
diffeomorphism 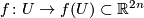 such that the restriction of
such that the restriction of  to
to  is equal to the pull-back
is equal to the pull-back 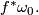 This implies that symplectic manifolds have
no local invariants.
This implies that symplectic manifolds have
no local invariants.
 An area form on an oriented surface is symplectic.
An area form on an oriented surface is symplectic.
 Let
Let  be a smooth manifold and let
be a smooth manifold and let  be a one-form on the cotangent bundle
be a one-form on the cotangent bundle 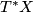 defined as follows.
If
defined as follows.
If  is a vector tangent to
is a vector tangent to 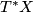 at a point
at a point  then
then 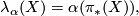 where
where
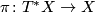 is the projection. In local coordinates the form
is the projection. In local coordinates the form  can be expressed as
can be expressed as
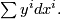 The differential
The differential 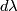 is a symplectic form on the cotangent bundle
is a symplectic form on the cotangent bundle 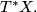
 If
If 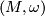 is a closed, i.e. compact and without boundary, symplectic
is a closed, i.e. compact and without boundary, symplectic  -manifold then the cohomology classes
-manifold then the cohomology classes
![[\omega]^k](/images/math/e/6/e/e6eff0918969467a4c56a4750f24fd36.png) are non-zero for
are non-zero for 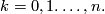 This follows from the fact that the cohomology class of the volume
form
This follows from the fact that the cohomology class of the volume
form 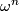 is nonzero on a closed manifold. This necessary condition implies that spheres of dimension greater than
two are not symplectic. More generally, no closed manifold of the form
is nonzero on a closed manifold. This necessary condition implies that spheres of dimension greater than
two are not symplectic. More generally, no closed manifold of the form 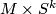 is symplectic for
is symplectic for 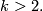
 The complex projective space
The complex projective space 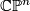 is symplectic with respect to its K\"ahler form.
Its pull back to a complex projective smooth manifold
is symplectic with respect to its K\"ahler form.
Its pull back to a complex projective smooth manifold 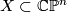 is also symplectic.
More generally, every K\"ahler manifold is symplectic.
is also symplectic.
More generally, every K\"ahler manifold is symplectic.
3 Symmetries
A diffeomorphism 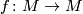 of a symplectic manifold
of a symplectic manifold 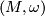 is called symplectic if it preserves
the symplectic form,
is called symplectic if it preserves
the symplectic form, 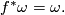 Sometimes such a diffeomorphism is called a symplectiomorphism.
The group of all symplectic diffeomorphisms of
Sometimes such a diffeomorphism is called a symplectiomorphism.
The group of all symplectic diffeomorphisms of 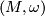 is denoted by
is denoted by
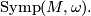
It follows from the nondegeneracy of the symplectic form  the map
the map 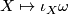 defines an isomorphism
between the vector fields and the one-forms on a symplectic manifold
defines an isomorphism
between the vector fields and the one-forms on a symplectic manifold 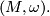 If the flow of a vector field
If the flow of a vector field  preserves the symplectic form we have that
preserves the symplectic form we have that 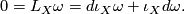 Then the closedness
of the symplectic form implies that the one-form
Then the closedness
of the symplectic form implies that the one-form 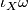 is closed. It follows that the Lie algebra of
the group of symplectic diffeomorhism consists of the vector fields
is closed. It follows that the Lie algebra of
the group of symplectic diffeomorhism consists of the vector fields  for which the one-form
for which the one-form 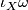 is closed. Hence it can be identified with the space of closed one-forms.
is closed. Hence it can be identified with the space of closed one-forms.
If the one-form 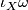 is exact, i.e.
is exact, i.e. 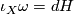 for some function
for some function 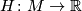 then the vector field
then the vector field  is called Hamiltonian. Symplectic diffeomorphism generated by Hamiltonian flows form
a group
is called Hamiltonian. Symplectic diffeomorphism generated by Hamiltonian flows form
a group 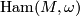 called the group of Hamiltonian diffeomorphism. Its Lie algebra can be
identified with the quotient of the space of smooth functions on
called the group of Hamiltonian diffeomorphism. Its Lie algebra can be
identified with the quotient of the space of smooth functions on  by the constants.
by the constants.
4 Constructions
4.1 Products
The product of symplectic manifolds 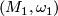 and
and 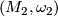 is a symplectic manifold with
respect to the form
is a symplectic manifold with
respect to the form 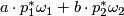 for nonzero real numbers
for nonzero real numbers
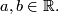 Here
Here 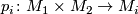 is the projection.
is the projection.
4.2 Bundles
A locally trivial bundle 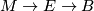 is called symplectic (resp. Hamiltonian) if its structure
group is a subgroup of the group of symplectic (resp. Hamiltonian) diffeomorphisms.
is called symplectic (resp. Hamiltonian) if its structure
group is a subgroup of the group of symplectic (resp. Hamiltonian) diffeomorphisms.
Example. The product of the Hopf bundle with the circle is a symplectic bundle 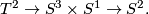 Indeed, the structure group is a group of rotations of the torus and hence it preserves the area.
As we have seen above the product
Indeed, the structure group is a group of rotations of the torus and hence it preserves the area.
As we have seen above the product 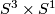 does not admit a symplectic form. This example
shows that, in general, the total space of a symplectic bundle is not symplectic.
does not admit a symplectic form. This example
shows that, in general, the total space of a symplectic bundle is not symplectic.
Let 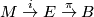 is a compact symplectic bundle over a symplectic base.
According to a theorem of Thurston, if there exists a cohomology class
is a compact symplectic bundle over a symplectic base.
According to a theorem of Thurston, if there exists a cohomology class 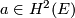 such that
its pull back to every fibre is equal to the class of the symplectic form of the fibre
then there exists a representative
such that
its pull back to every fibre is equal to the class of the symplectic form of the fibre
then there exists a representative  of the class
of the class  such that
such that
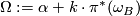 is a symplectic form on
is a symplectic form on  for every big enough
for every big enough 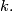
A symplectic fiber bundle may have a symplectic form on the total space which restricts symplectically to the fibers, even if the base is not symplectic. Such bundles are constructed using fat connections. Let there be given a principal fiber bundle
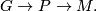
Let 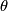 be a connection form,
be a connection form, 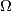 the curvature form of this connection, and
the curvature form of this connection, and 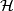 be the horizontal distribution. A vector
be the horizontal distribution. A vector 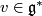 is called fat (with respect to the given connection), if the 2-form
is called fat (with respect to the given connection), if the 2-form
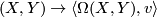
is nondegenerate on the horizontal distribution of the connection. The following theorem yields a construction of a symplectic form on the total space of fiber bundles associated with principal bundles equipped with particular connections.
Theorem 3.1. Let there be given a symplectic manifold 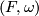 endowed with a hamiltonian action of a Lie group
endowed with a hamiltonian action of a Lie group  . Let
. Let 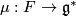 be the moment map of the
be the moment map of the  -action. If
-action. If 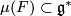 consists of fat vectors, then the associated bundle
consists of fat vectors, then the associated bundle
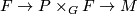
admits a fiberwise symplectic form on the total space.
using this theorem, one can construct examples of symplectic fiber bundles with fiberwise symplectic form on the total space (see examples below).
Example (twistor bundles)
Consider the principal bundle of the orthogonal frame bundles over  -dimensional manifold
-dimensional manifold  :
:
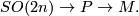
Let 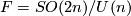 . The associated bundle with fiber
. The associated bundle with fiber 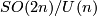 is called the twistor bundle. It is easy to see that
is called the twistor bundle. It is easy to see that 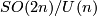 can be identified with a coadjoint orbit
can be identified with a coadjoint orbit 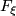 of some
of some 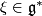 , where
, where 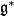 denotes the Lie algebra of
denotes the Lie algebra of 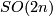 . Moreover, if
. Moreover, if  admits Riemannian metric of pinched curvature with sufficiently small pinching constant then
admits Riemannian metric of pinched curvature with sufficiently small pinching constant then  is fat with respect to the Levi-Civitta connection in the frame bundle. As a result, the whole coadjoint orbit (which is the image of the moment map of the
is fat with respect to the Levi-Civitta connection in the frame bundle. As a result, the whole coadjoint orbit (which is the image of the moment map of the 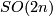 -action) consists of fat vectors. Thus, we obtain a fiberwise symplectic structure on the total space of any twistor bundle
-action) consists of fat vectors. Thus, we obtain a fiberwise symplectic structure on the total space of any twistor bundle
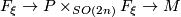
over even-dimensional manifolds of pinched curvature. In particular, twistor bundles over spheres 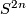 or hyperbolic manifolds, admit fiberwise symplectic structures. The simplest example of this construction is the fibering of
or hyperbolic manifolds, admit fiberwise symplectic structures. The simplest example of this construction is the fibering of 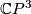 over
over  with fiber
with fiber 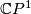 , since it is known that the total space of the twistor bundle over
, since it is known that the total space of the twistor bundle over  is
is 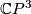 .
.
Example (locally homogeneous complex manifolds)
Let  be a Lie group of non-compact type, which is a real form of a complex Lie group
be a Lie group of non-compact type, which is a real form of a complex Lie group 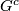 . Choose a parabolic subgroup
. Choose a parabolic subgroup 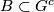 and a maximal compact subgroup
and a maximal compact subgroup  in
in  . Assume that
. Assume that 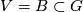 is compact. Then one can show that
is compact. Then one can show that 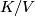 can be identified with a coadjoint orbit of some vector in
can be identified with a coadjoint orbit of some vector in 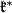 , which is fat with respect to a
, which is fat with respect to a  -invariant connection in the principal bundle
-invariant connection in the principal bundle
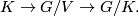
It follows that the associated bundle
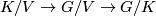
is a symplectic fiber bundle with fiberwise symplectic structure. This construction can be compactified by taking lattices in  which intersect trivially with
which intersect trivially with  . A particular example is given by the fiber bundle
. A particular example is given by the fiber bundle
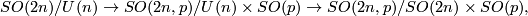
and its compactification by lattices.
4.3 Symplectic reduction
Let  be a Lie group acting on a symplectic manifold
be a Lie group acting on a symplectic manifold 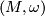 in a hamiltonian way. Denote
by
in a hamiltonian way. Denote
by 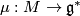 the moment map of this action. Since
the moment map of this action. Since  acts on the level set
acts on the level set
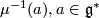 , one can consider the orbit space
, one can consider the orbit space 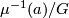 . It is an orbifold in general, but it happens to be a manifold, when
. It is an orbifold in general, but it happens to be a manifold, when  acts freely on the preimage, and
acts freely on the preimage, and  is a regular point. In this case,
is a regular point. In this case, 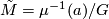 is a symplectic manifold as well, called symplectic reduction. It is often denoted by
is a symplectic manifold as well, called symplectic reduction. It is often denoted by 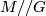 .
.
4.4 Symplectic cut
Let 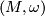 be a symplectic manifold with a hamiltonian action of the circle
be a symplectic manifold with a hamiltonian action of the circle 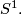 If
If 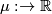 is the moment map,
is the moment map, 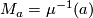 is a regular level, then the action restricted to
is a regular level, then the action restricted to 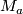 has no fixed points, hence
has no fixed points, hence 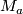 is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs.
is the boundary of the associated disk bundle W. This is a manifold if the action is free and an orbifold if a non-trivial isotropy occurs.
4.5 Coadjoint orbits
4.6 Symplectic homogeneous spaces
Nilmanifolds, solvmanifolds, homogeneous spaces of semisimple Lie groups
4.7 Donaldson's theorem on submanifolds
4.8 Surgery in codimension 2
Consider two symplectic manifolds 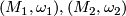 of equal dimension and suppose that there are codimension two symplectic submanifolds
of equal dimension and suppose that there are codimension two symplectic submanifolds 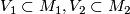 and a symplectomorphism
and a symplectomorphism 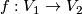 such that Chern classes of normal bundles satisfy
such that Chern classes of normal bundles satisfy 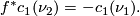 Then by removing tubular neighborhods of
Then by removing tubular neighborhods of 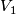 and
and 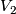 we get manifolds with boundaries. The map
we get manifolds with boundaries. The map  induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with
induces a diffeomorphism of the boundaries, one can form a new manifold identifying the boundaries by this diffeomorphism and define on it a symplectic form which coincides with
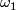 and
and 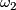 outside of a tubular neigborhood of the trace of glueing [Gompf1995]. The same works if
outside of a tubular neigborhood of the trace of glueing [Gompf1995]. The same works if 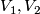 are symplectic submanifolds of a connected symplectic manifold.
are symplectic submanifolds of a connected symplectic manifold.
4.9 Symplectic blow-up
5 Invariants
...
6 Classification/Characterization
...
7 Further discussion
...
8 References
- [Gompf1995] R. E. Gompf, A new construction of symplectic manifolds, Ann. of Math. (2) 142 (1995), no.3, 527–595. MR1356781 (96j:57025) Zbl 0849.53027
- [McDuff&Salamon1998] D. McDuff and D. Salamon, Introduction to symplectic topology, The Clarendon Press Oxford University Press, 1998. MR1698616 (2000g:53098) Zbl 0978.53120