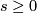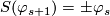Suspension of a symmetric complex (Ex)
(Difference between revisions)
Tibor Macko (Talk | contribs) (Created page with "<wikitex>; Using the definition and the $\omega$ from Exercise 4 show that $$ S(\varphi)_0 = 0 $$ and $$ S(\varphi_{s+1}) = \pm \varphi_s $$ </wikitex> == References == {{#Ref...") |
Tibor Macko (Talk | contribs) |
||
| Line 4: | Line 4: | ||
S(\varphi)_0 = 0 | S(\varphi)_0 = 0 | ||
$$ | $$ | ||
| − | and | + | and for $s \geq 0$ |
$$ | $$ | ||
S(\varphi_{s+1}) = \pm \varphi_s | S(\varphi_{s+1}) = \pm \varphi_s | ||
Revision as of 12:48, 25 August 2013
Using the definition and the  from Exercise 4 show that
from Exercise 4 show that
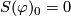
and for