Surgery obstruction map I (Ex)
From Manifold Atlas
(Difference between revisions)
| Line 11: | Line 11: | ||
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| − | [[Category:Exercises | + | [[Category:Exercises with solution]] |
Latest revision as of 22:49, 29 May 2012
Show that the surgery obstruction map
![\displaystyle \theta \colon \mathcal{N} (X) \rightarrow L_{n} (\Zz [\pi_1 (X)])](/images/math/6/9/c/69c7b69a4f9af6be92d40031eb894159.png)
is not in general a homomorphism of abelian groups, when the normal invariants are viewed as an abelian group with the group structure coming from the Whitney sum of vector bundles.
Hint: in the simply connected case and 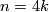 , find a formula for
, find a formula for 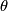 in terms of the
in terms of the 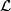 -class. See Exercise 13.3 in [Ranicki2002].
-class. See Exercise 13.3 in [Ranicki2002].
References
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001