Surgery obstruction groups

From Manifold Atlas

Jump to: navigation, search

The user responsible for this page is Hambleton. No other user may edit this page at present.

This page has not been refereed. The information given here might be incomplete or provisional.

1 Introduction

The surgery obstruction groups 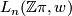$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}L_n(\bZ\pi, w)$ of C.T.C. Wall [Wall1999], [Wall1976] contain the obstructions to doing surgery on a degree 1 normal map 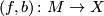$(f,b)\colon M \to X$ to obtain a homotopy equivalence. 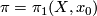In this setting, $X$ is an $n$ -dimensional Poincaré complex $\pi = \pi_1(X, x_0)$ is the fundamental group of $X$ , and $w$ is the orientation character of $X$ , which is determined by the first Stiefel-Whitney class of $X$ , $w_1(X)$ .

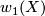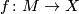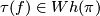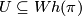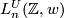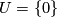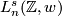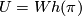A homotopy equivalence $f\colon M \to X$ has a Whitehead torsion $\tau(f) \in Wh(\pi)$ in the Whitehead group of $\pi$ . The surgery obstruction groups for surgery up to a homotopy equivalence with torsion in a prescribed subgroup $U \subseteq Wh(\pi)$ are denoted $L^U_n(\bZ, w)$ . 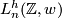The most important cases for geometric applications are $U = \{ 0 \}$ , denoted $L^s_n(\bZ, w)$ , or $U = Wh(\pi)$ , denoted $L^h_n(\bZ, w)$ . The main problems are the following:

to develop methods for the computation of the surgery obstruction groups,
to define invariants of degree 1 normal maps which detect the surgery obstruction.

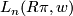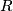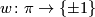The surgery obstruction groups $L_n(R\pi, w)$ depend on a coefficient ring $R$ , a discrete group $\pi$ and an orientation character $w\colon \pi \to \{\pm 1\}$ . In general the surgery obstruction groups are abelian groups. For finite groups $\pi$ the $L$ -groups are finitely-generated and the only torsion is $2$ -primary.