Super manifolds: an incomplete survey
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:56, 1 April 2011 and the changes since publication. |
We present an incomplete survey on some basic notions of super manifolds which may serve as a short introduction to this subject. Almost all the material is taken from the beautiful survey article on super manifolds [Deligne&Morgan1999]. Standard references also include [Leites1980], [Berezin1987], [Manin1988] or [Voronov1991]. The material below is a prerequisite to our papers [Hohnhold&Kreck&Stolz&Teichner2010] and [Stolz&Teichner2008].
Contents |
1 Super Algebra
Tex syntax error-graded vector spaces, with the graded tensor product. As a consequence, a super algebra is simply a monoidal object in this category and is hence the same thing as a
Tex syntax error-graded algebra. For example, the endomorphism ring
Tex syntax errorof a super vector space
 inherits a natural
inherits a natural Tex syntax error-grading from that of
 . The distinction between these notions only arises from the choice of symmetry operators
. The distinction between these notions only arises from the choice of symmetry operators
Tex syntax error
There are two standard choices, yielding two very different symmetric monoidal categories. For super vector spaces one has
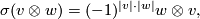
Tex syntax erroris the
Tex syntax error-degree of a homogenous vector
Tex syntax error. For
Tex syntax error-graded vector spaces the signs would be omitted. This basic difference is sometimes summarized as the
Tex syntax errorSign rule: Commuting two odd quantities yields a sign
 .
As a consequence, a super algebra is commutative if for all homogenenous
.
As a consequence, a super algebra is commutative if for all homogenenous Tex syntax errorwe have
Tex syntax error
Tex syntax error-graded algebra. The standard examples of commutative super algebras are the exterior algebras
Tex syntax error. As we shall see, the generators of
Tex syntax erroryield the so-called odd coordinates on super manifolds; these anti-commute and hence are useful when trying to describe physical systems involving Fermions. Super algebras also arise naturally in algebraic topology: for every space
 , the cohomology ring
, the cohomology ring Tex syntax erroris a commutative super algebra. Let
 be a commutative super algebra. The derivations of
be a commutative super algebra. The derivations of  are endomorphisms
are endomorphisms Tex syntax errorsatisfying the Leibniz rule: [1]
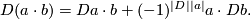
Tex syntax erroris a super Lie algebra with respect to the bracket operation
![\displaystyle [D,E] := DE - (-1)^{|D| |E|}ED](/images/math/f/a/b/fabce79898f93e07c6541fe82853532a.png)
Tex syntax error.
 together with a Lie bracket
together with a Lie bracket ![[\cdot, \cdot]: L\otimes L\to L](/images/math/6/1/5/615ad7472d37b5dff1fb18d6b71dbc62.png) that is skew symmetric
that is skew symmetric ![\displaystyle [ D,E ] + (-1)^{|D| |E|} [ E,D ] = 0](/images/math/6/c/1/6c1f534b9f85a41f1abe28df4b859fc4.png)
![\displaystyle [D, [ E,F ]] + (-1)^{|D| (|E| + |F|)} [ E, [F,D ]] + (-1)^{|F| (|D| + |E|)} [ F, [ D,E ]] = 0.](/images/math/f/5/9/f595128d405d34d21d951cb31b74b3c6.png)
Note that we cyclically permuted the 3 symbols and put down the signs according to the above sign rule.
2 Super Manifolds
Tex syntax erroris
Tex syntax errorequipped with the sheaf
Tex syntax errorof commutative super
Tex syntax error-algebras
Tex syntax error.
 of dimension
of dimension Tex syntax erroris a pair
Tex syntax errorconsisting of a (Hausdorff and second countable) topological space
Tex syntax errortogether with a sheaf of commutative super
Tex syntax error-algebras
Tex syntax errorthat is locally isomorphic to
Tex syntax error. A morphism
Tex syntax errorbetween super manifolds
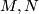 is defined to be a continuous map
is defined to be a continuous map Tex syntax error, together with a map
 of sheaves covering
of sheaves covering Tex syntax error. More precisely, for every open subset
Tex syntax errorthere are algebra maps
Tex syntax error
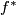 for
for  and we denote this category of super manifolds by
and we denote this category of super manifolds by Tex syntax error.
 there is an associated reduced manifold
there is an associated reduced manifold 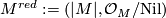
Tex syntax errorand there is an inclusion of super manifolds
Tex syntax error. Note that the sheaf of ideals
Tex syntax erroris generated by odd functions. Other geometric super objects can be defined in a similar way. For example, replacing
Tex syntax errorby
Tex syntax errorand
Tex syntax errorby analytic functions one obtains complex (analytic) super manifolds. There is also an important notion of cs manifolds. These are spaces equipped with sheaves of commutative super
Tex syntax error-algebras that locally look like
Tex syntax error. One relevance of cs manifolds is that they appear naturally as the smooth super manifolds underlying complex analytic super manifolds. In our work, cs manifolds are essential to define the notion of a unitary field theory but this is not relevant for the current discussion.
Example 2.2.
Let be a real vector bundle of fiber dimension
be a real vector bundle of fiber dimension  over the ordinary manifold
over the ordinary manifold Tex syntax errorand
Tex syntax errorthe associated algebra bundle of alternating multilinear forms on
 . Then its sheaf of sections gives a super manifold
. Then its sheaf of sections gives a super manifold Tex syntax errorof dimension
Tex syntax error, denoted by
Tex syntax error. In the current smooth setting, Marjorie Batchelor proved in [Batchelor1979] that every super manifold is isomorphic to one of this type (this is not true for analytic super manifolds). More precisely, let
Tex syntax errordenote the category of real vector bundles over smooth manifolds, and for
Tex syntax error, consider the vector bundle
Tex syntax errorover
Tex syntax errorwith sheaf of sections
Tex syntax error. Then the functors
Tex syntax error
Tex syntax errorbut there are only non-natural isomorphisms
Tex syntax error, coming from a choice of a partition of unity. In other words, these functors induce a bijection on isomorphism classes of objects and inclusions on morphisms but they are not equivalences of categories because there are many more morphims in
Tex syntax errorthan the linear bundle maps coming from
Tex syntax error.
Tex syntax errorfor the algebra of (global) functions on a super manifold
 .
.
Proposition 2.3.
ForTex syntax error, the functor
Tex syntax errorinduces natural bijections
Tex syntax error
Tex syntax erroris an open super submanifold (a
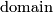 ),
), Tex syntax erroris in bijective correspondence with those
Tex syntax errorin
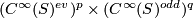 that satisfy
that satisfy
Tex syntax error
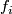 ,
, Tex syntax errorare called the coordinates of
Tex syntax errordefined by
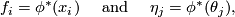
Tex syntax errorare coordinates on
Tex syntax error. Moreover, by the first part we see that
Tex syntax errorand hence
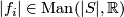 .
.
The proof of the first part is based on the existence of partitions of unity for super manifolds, so it is false in analytic settings. The second part always holds and is proved in [Leites1980].
3 The Functor of Points
 -points, i.e. instead of
-points, i.e. instead of  itself one considers the morphism sets
itself one considers the morphism sets Tex syntax error, where
 varies over all super manifolds
varies over all super manifolds  . More formally, embed the category
. More formally, embed the category Tex syntax errorof super manifolds in the category of contravariant functors from
Tex syntax errorto
Tex syntax errorby
Tex syntax error
Tex syntax errorwith the the category of representable functors, defined to be those in the image of
 . We will sometimes refer to an arbitrary functor
. We will sometimes refer to an arbitrary functor Tex syntax erroras a generalized super manifold. Note that Proposition 2.3 makes it easy to describe the morphism sets
Tex syntax error. We'd also like to point out that the functor of points approach is closely related to computations involving additional odd quantities (the odd coordinates of
 as opposed to those of
as opposed to those of  ) in many physics papers.
) in many physics papers.
4 Super Lie Groups
Tex syntax error. According to the functor of points approach, such a group object in
Tex syntax errorcan be described by giving a functor
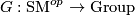 such that the composition with the forgetful functor
such that the composition with the forgetful functor 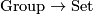 is representable.
is representable.
Example 4.1.
The simplest super Lie group is the additive group structure on 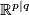 . It is given by the following composition law on
. It is given by the following composition law on 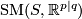 , obviously natural in
, obviously natural in  :
:
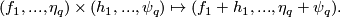
The super general linear group 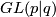 is defined by
is defined by
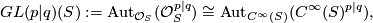
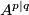 denotes the
denotes the  -module freely generated by
-module freely generated by  even and
even and  odd generators. We need to check that this is representable. We claim that
odd generators. We need to check that this is representable. We claim that 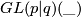 is represented by the open super submanifold
is represented by the open super submanifold 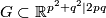 characterized by
characterized by 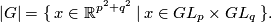
This follows directly from proposition 2.3 using that a map between super algebras is invertible if and only if it is invertible modulo nilpotent elements.
5 Super Vector Bundles
 is a locally free sheaf
is a locally free sheaf 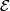 of
of Tex syntax error-modules of dimension
Tex syntax error. The most basic example of a super vector bundle is the tangent bundle of a super manifold
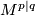 . It is the sheaf of
. It is the sheaf of Tex syntax error-modules
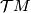 defined by
defined by
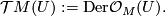
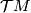 is locally free of dimension
is locally free of dimension Tex syntax error: If
 are local coordinates on
are local coordinates on  , then a local basis is given by
, then a local basis is given by  . Note that there is also a linear fibre bundle
. Note that there is also a linear fibre bundle 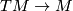 with structure group
with structure group 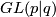 , where
, where  is a super manifold of dimension
is a super manifold of dimension 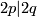 . More generally, any vector bundle
. More generally, any vector bundle 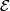 over
over  has a total space
has a total space 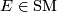 that comes with a projection map
that comes with a projection map 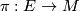 . It can be most easily described in terms of its
. It can be most easily described in terms of its  -points
-points
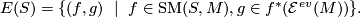
So  is an even global section of the pullback bundle on
is an even global section of the pullback bundle on  and the projection
and the projection  comes from forgetting this datum. To prove that this functor
comes from forgetting this datum. To prove that this functor 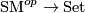 is representable one uses the local triviality of
is representable one uses the local triviality of 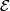 and Proposition 2.3. It follows by construction that the typical fibre of the projection
and Proposition 2.3. It follows by construction that the typical fibre of the projection  is
is 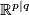 and the structure group is
and the structure group is 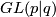 .
.
 . It is an involution
. It is an involution 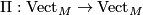
 with grading involution
with grading involution  to
to 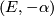 . This means that even and odd parts are exchanged. To define
. This means that even and odd parts are exchanged. To define 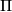 on morphisms it is easiest to give it as
on morphisms it is easiest to give it as 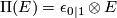 , where
, where 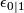 is the trivial bundle of dimension
is the trivial bundle of dimension 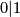 (aka the constant sheaf of free
(aka the constant sheaf of free Tex syntax error-modules).
One can define the super Lie algebra 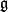 of a super Lie group
of a super Lie group  as follows. A vector field
as follows. A vector field 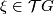 is called left-invariant if
is called left-invariant if  is related to itself under the left-translation by all
is related to itself under the left-translation by all 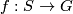 :
:
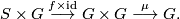
 as a vertical vector field on
as a vertical vector field on 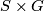 in the obvious way. The super Lie algebra
in the obvious way. The super Lie algebra 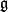 consists of all left-invariant vector fields on
consists of all left-invariant vector fields on  . Pulling back via the unit
. Pulling back via the unit 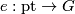 defines an isomorphism
defines an isomorphism 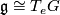 , in particular, the vector space dimension of
, in particular, the vector space dimension of 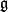 is
is Tex syntax error.
6 Footnotes
- ↑ Whenever we write formulas involving the degree
 of certain elements, we implicitly assume that these elements are homogenous.
of certain elements, we implicitly assume that these elements are homogenous.
7 References
- [Batchelor1979] M. Batchelor, The structure of supermanifolds, Trans. Amer. Math. Soc. 253 (1979), 329–338. MR536951 (80h:58002) Zbl 0413.58002
- [Berezin1987] F. A. Berezin, Introduction to algebra and analysis with anticommuting variables, Reidel 1987.
- [Deligne&Morgan1999] P. Deligne and J. W. Morgan, Notes on supersymmetry (following Joseph Bernstein), Quantum fields and strings: a course for mathematicians, Vol. 1, 2 (Princeton, NJ, 1996/1997), 41–97, Amer. Math. Soc., Providence, RI, (1999), 41–97. MR1701597 (2001g:58007) Zbl 1170.58302
- [Hohnhold&Kreck&Stolz&Teichner2010] H. Hohnhold, M. Kreck, S. Stolz and P. Teichner, Differential Forms and 0-dimensional Super Symmetric Field Theories, to appear in Quantum Topology, Journal of the European Math. Soc. (2010).
- [Leites1980] D. A. Leites, Introduction to the theory of supermanifolds, Russian Math. Surveys 35 No 1 (1980), 3–57. MR0565567 (81j:58003) Zbl 0439.58007
- [Manin1988] Y. I. Manin, Gauge field theory and complex geometry, Springer-Verlag, Berlin, 1988. MR954833 (89d:32001) Zbl 0884.53002
- [Stolz&Teichner2008] S. Stolz and P. Teichner, Supersymmetric Euclidean field theories and generalized cohomology, Survey (2008). Available at http://math.berkeley.edu/~teichner/Papers/Survey.pdf.
- [Voronov1991] T. Voronov, Geometric integration theory on supermanifolds, Harwood Academic Publishers, Chur, 1991. MR1202882 (95b:58023) Zbl 0839.58014
8 External links
- The Wikipedia page on Super manifolds.
Tex syntax error-graded algebra. For example, the endomorphism ring
Tex syntax errorof a super vector space
 inherits a natural
inherits a natural Tex syntax error-grading from that of
 . The distinction between these notions only arises from the choice of symmetry operators
. The distinction between these notions only arises from the choice of symmetry operators
Tex syntax error
There are two standard choices, yielding two very different symmetric monoidal categories. For super vector spaces one has
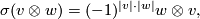
Tex syntax erroris the
Tex syntax error-degree of a homogenous vector
Tex syntax error. For
Tex syntax error-graded vector spaces the signs would be omitted. This basic difference is sometimes summarized as the
Tex syntax errorSign rule: Commuting two odd quantities yields a sign
 .
As a consequence, a super algebra is commutative if for all homogenenous
.
As a consequence, a super algebra is commutative if for all homogenenous Tex syntax errorwe have
Tex syntax error
Tex syntax error-graded algebra. The standard examples of commutative super algebras are the exterior algebras
Tex syntax error. As we shall see, the generators of
Tex syntax erroryield the so-called odd coordinates on super manifolds; these anti-commute and hence are useful when trying to describe physical systems involving Fermions. Super algebras also arise naturally in algebraic topology: for every space
 , the cohomology ring
, the cohomology ring Tex syntax erroris a commutative super algebra. Let
 be a commutative super algebra. The derivations of
be a commutative super algebra. The derivations of  are endomorphisms
are endomorphisms Tex syntax errorsatisfying the Leibniz rule: [1]
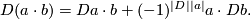
Tex syntax erroris a super Lie algebra with respect to the bracket operation
![\displaystyle [D,E] := DE - (-1)^{|D| |E|}ED](/images/math/f/a/b/fabce79898f93e07c6541fe82853532a.png)
Tex syntax error.
 together with a Lie bracket
together with a Lie bracket ![[\cdot, \cdot]: L\otimes L\to L](/images/math/6/1/5/615ad7472d37b5dff1fb18d6b71dbc62.png) that is skew symmetric
that is skew symmetric ![\displaystyle [ D,E ] + (-1)^{|D| |E|} [ E,D ] = 0](/images/math/6/c/1/6c1f534b9f85a41f1abe28df4b859fc4.png)
![\displaystyle [D, [ E,F ]] + (-1)^{|D| (|E| + |F|)} [ E, [F,D ]] + (-1)^{|F| (|D| + |E|)} [ F, [ D,E ]] = 0.](/images/math/f/5/9/f595128d405d34d21d951cb31b74b3c6.png)
Note that we cyclically permuted the 3 symbols and put down the signs according to the above sign rule.
2 Super Manifolds
Tex syntax erroris
Tex syntax errorequipped with the sheaf
Tex syntax errorof commutative super
Tex syntax error-algebras
Tex syntax error.
 of dimension
of dimension Tex syntax erroris a pair
Tex syntax errorconsisting of a (Hausdorff and second countable) topological space
Tex syntax errortogether with a sheaf of commutative super
Tex syntax error-algebras
Tex syntax errorthat is locally isomorphic to
Tex syntax error. A morphism
Tex syntax errorbetween super manifolds
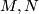 is defined to be a continuous map
is defined to be a continuous map Tex syntax error, together with a map
 of sheaves covering
of sheaves covering Tex syntax error. More precisely, for every open subset
Tex syntax errorthere are algebra maps
Tex syntax error
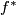 for
for  and we denote this category of super manifolds by
and we denote this category of super manifolds by Tex syntax error.
 there is an associated reduced manifold
there is an associated reduced manifold 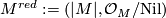
Tex syntax errorand there is an inclusion of super manifolds
Tex syntax error. Note that the sheaf of ideals
Tex syntax erroris generated by odd functions. Other geometric super objects can be defined in a similar way. For example, replacing
Tex syntax errorby
Tex syntax errorand
Tex syntax errorby analytic functions one obtains complex (analytic) super manifolds. There is also an important notion of cs manifolds. These are spaces equipped with sheaves of commutative super
Tex syntax error-algebras that locally look like
Tex syntax error. One relevance of cs manifolds is that they appear naturally as the smooth super manifolds underlying complex analytic super manifolds. In our work, cs manifolds are essential to define the notion of a unitary field theory but this is not relevant for the current discussion.
Example 2.2.
Let be a real vector bundle of fiber dimension
be a real vector bundle of fiber dimension  over the ordinary manifold
over the ordinary manifold Tex syntax errorand
Tex syntax errorthe associated algebra bundle of alternating multilinear forms on
 . Then its sheaf of sections gives a super manifold
. Then its sheaf of sections gives a super manifold Tex syntax errorof dimension
Tex syntax error, denoted by
Tex syntax error. In the current smooth setting, Marjorie Batchelor proved in [Batchelor1979] that every super manifold is isomorphic to one of this type (this is not true for analytic super manifolds). More precisely, let
Tex syntax errordenote the category of real vector bundles over smooth manifolds, and for
Tex syntax error, consider the vector bundle
Tex syntax errorover
Tex syntax errorwith sheaf of sections
Tex syntax error. Then the functors
Tex syntax error
Tex syntax errorbut there are only non-natural isomorphisms
Tex syntax error, coming from a choice of a partition of unity. In other words, these functors induce a bijection on isomorphism classes of objects and inclusions on morphisms but they are not equivalences of categories because there are many more morphims in
Tex syntax errorthan the linear bundle maps coming from
Tex syntax error.
Tex syntax errorfor the algebra of (global) functions on a super manifold
 .
.
Proposition 2.3.
ForTex syntax error, the functor
Tex syntax errorinduces natural bijections
Tex syntax error
Tex syntax erroris an open super submanifold (a
 ),
), Tex syntax erroris in bijective correspondence with those
Tex syntax errorin
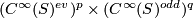 that satisfy
that satisfy
Tex syntax error
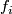 ,
, Tex syntax errorare called the coordinates of
Tex syntax errordefined by
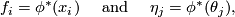
Tex syntax errorare coordinates on
Tex syntax error. Moreover, by the first part we see that
Tex syntax errorand hence
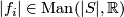 .
.
The proof of the first part is based on the existence of partitions of unity for super manifolds, so it is false in analytic settings. The second part always holds and is proved in [Leites1980].
3 The Functor of Points
 -points, i.e. instead of
-points, i.e. instead of  itself one considers the morphism sets
itself one considers the morphism sets Tex syntax error, where
 varies over all super manifolds
varies over all super manifolds  . More formally, embed the category
. More formally, embed the category Tex syntax errorof super manifolds in the category of contravariant functors from
Tex syntax errorto
Tex syntax errorby
Tex syntax error
Tex syntax errorwith the the category of representable functors, defined to be those in the image of
 . We will sometimes refer to an arbitrary functor
. We will sometimes refer to an arbitrary functor Tex syntax erroras a generalized super manifold. Note that Proposition 2.3 makes it easy to describe the morphism sets
Tex syntax error. We'd also like to point out that the functor of points approach is closely related to computations involving additional odd quantities (the odd coordinates of
 as opposed to those of
as opposed to those of  ) in many physics papers.
) in many physics papers.
4 Super Lie Groups
Tex syntax error. According to the functor of points approach, such a group object in
Tex syntax errorcan be described by giving a functor
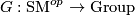 such that the composition with the forgetful functor
such that the composition with the forgetful functor 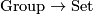 is representable.
is representable.
Example 4.1.
The simplest super Lie group is the additive group structure on 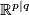 . It is given by the following composition law on
. It is given by the following composition law on 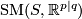 , obviously natural in
, obviously natural in  :
:
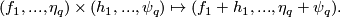
The super general linear group 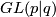 is defined by
is defined by
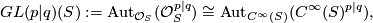
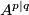 denotes the
denotes the  -module freely generated by
-module freely generated by  even and
even and  odd generators. We need to check that this is representable. We claim that
odd generators. We need to check that this is representable. We claim that 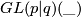 is represented by the open super submanifold
is represented by the open super submanifold 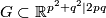 characterized by
characterized by 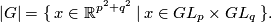
This follows directly from proposition 2.3 using that a map between super algebras is invertible if and only if it is invertible modulo nilpotent elements.
5 Super Vector Bundles
 is a locally free sheaf
is a locally free sheaf 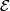 of
of Tex syntax error-modules of dimension
Tex syntax error. The most basic example of a super vector bundle is the tangent bundle of a super manifold
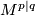 . It is the sheaf of
. It is the sheaf of Tex syntax error-modules
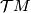 defined by
defined by
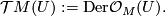
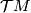 is locally free of dimension
is locally free of dimension Tex syntax error: If
 are local coordinates on
are local coordinates on  , then a local basis is given by
, then a local basis is given by  . Note that there is also a linear fibre bundle
. Note that there is also a linear fibre bundle 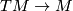 with structure group
with structure group 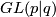 , where
, where  is a super manifold of dimension
is a super manifold of dimension 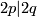 . More generally, any vector bundle
. More generally, any vector bundle 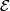 over
over  has a total space
has a total space 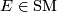 that comes with a projection map
that comes with a projection map 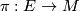 . It can be most easily described in terms of its
. It can be most easily described in terms of its  -points
-points
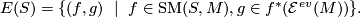
So  is an even global section of the pullback bundle on
is an even global section of the pullback bundle on  and the projection
and the projection  comes from forgetting this datum. To prove that this functor
comes from forgetting this datum. To prove that this functor 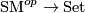 is representable one uses the local triviality of
is representable one uses the local triviality of 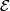 and Proposition 2.3. It follows by construction that the typical fibre of the projection
and Proposition 2.3. It follows by construction that the typical fibre of the projection  is
is 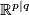 and the structure group is
and the structure group is 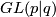 .
.
 . It is an involution
. It is an involution 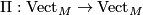
 with grading involution
with grading involution  to
to 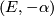 . This means that even and odd parts are exchanged. To define
. This means that even and odd parts are exchanged. To define 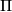 on morphisms it is easiest to give it as
on morphisms it is easiest to give it as 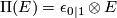 , where
, where 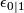 is the trivial bundle of dimension
is the trivial bundle of dimension 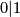 (aka the constant sheaf of free
(aka the constant sheaf of free Tex syntax error-modules).
One can define the super Lie algebra 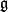 of a super Lie group
of a super Lie group  as follows. A vector field
as follows. A vector field 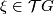 is called left-invariant if
is called left-invariant if  is related to itself under the left-translation by all
is related to itself under the left-translation by all 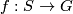 :
:
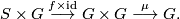
 as a vertical vector field on
as a vertical vector field on 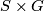 in the obvious way. The super Lie algebra
in the obvious way. The super Lie algebra 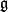 consists of all left-invariant vector fields on
consists of all left-invariant vector fields on  . Pulling back via the unit
. Pulling back via the unit 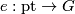 defines an isomorphism
defines an isomorphism 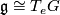 , in particular, the vector space dimension of
, in particular, the vector space dimension of 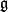 is
is Tex syntax error.
6 Footnotes
- ↑ Whenever we write formulas involving the degree
 of certain elements, we implicitly assume that these elements are homogenous.
of certain elements, we implicitly assume that these elements are homogenous.
7 References
- [Batchelor1979] M. Batchelor, The structure of supermanifolds, Trans. Amer. Math. Soc. 253 (1979), 329–338. MR536951 (80h:58002) Zbl 0413.58002
- [Berezin1987] F. A. Berezin, Introduction to algebra and analysis with anticommuting variables, Reidel 1987.
- [Deligne&Morgan1999] P. Deligne and J. W. Morgan, Notes on supersymmetry (following Joseph Bernstein), Quantum fields and strings: a course for mathematicians, Vol. 1, 2 (Princeton, NJ, 1996/1997), 41–97, Amer. Math. Soc., Providence, RI, (1999), 41–97. MR1701597 (2001g:58007) Zbl 1170.58302
- [Hohnhold&Kreck&Stolz&Teichner2010] H. Hohnhold, M. Kreck, S. Stolz and P. Teichner, Differential Forms and 0-dimensional Super Symmetric Field Theories, to appear in Quantum Topology, Journal of the European Math. Soc. (2010).
- [Leites1980] D. A. Leites, Introduction to the theory of supermanifolds, Russian Math. Surveys 35 No 1 (1980), 3–57. MR0565567 (81j:58003) Zbl 0439.58007
- [Manin1988] Y. I. Manin, Gauge field theory and complex geometry, Springer-Verlag, Berlin, 1988. MR954833 (89d:32001) Zbl 0884.53002
- [Stolz&Teichner2008] S. Stolz and P. Teichner, Supersymmetric Euclidean field theories and generalized cohomology, Survey (2008). Available at http://math.berkeley.edu/~teichner/Papers/Survey.pdf.
- [Voronov1991] T. Voronov, Geometric integration theory on supermanifolds, Harwood Academic Publishers, Chur, 1991. MR1202882 (95b:58023) Zbl 0839.58014
8 External links
- The Wikipedia page on Super manifolds.
Tex syntax error-graded algebra. For example, the endomorphism ring
Tex syntax errorof a super vector space
 inherits a natural
inherits a natural Tex syntax error-grading from that of
 . The distinction between these notions only arises from the choice of symmetry operators
. The distinction between these notions only arises from the choice of symmetry operators
Tex syntax error
There are two standard choices, yielding two very different symmetric monoidal categories. For super vector spaces one has
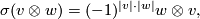
Tex syntax erroris the
Tex syntax error-degree of a homogenous vector
Tex syntax error. For
Tex syntax error-graded vector spaces the signs would be omitted. This basic difference is sometimes summarized as the
Tex syntax errorSign rule: Commuting two odd quantities yields a sign
 .
As a consequence, a super algebra is commutative if for all homogenenous
.
As a consequence, a super algebra is commutative if for all homogenenous Tex syntax errorwe have
Tex syntax error
Tex syntax error-graded algebra. The standard examples of commutative super algebras are the exterior algebras
Tex syntax error. As we shall see, the generators of
Tex syntax erroryield the so-called odd coordinates on super manifolds; these anti-commute and hence are useful when trying to describe physical systems involving Fermions. Super algebras also arise naturally in algebraic topology: for every space
 , the cohomology ring
, the cohomology ring Tex syntax erroris a commutative super algebra. Let
 be a commutative super algebra. The derivations of
be a commutative super algebra. The derivations of  are endomorphisms
are endomorphisms Tex syntax errorsatisfying the Leibniz rule: [1]
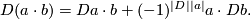
Tex syntax erroris a super Lie algebra with respect to the bracket operation
![\displaystyle [D,E] := DE - (-1)^{|D| |E|}ED](/images/math/f/a/b/fabce79898f93e07c6541fe82853532a.png)
Tex syntax error.
 together with a Lie bracket
together with a Lie bracket ![[\cdot, \cdot]: L\otimes L\to L](/images/math/6/1/5/615ad7472d37b5dff1fb18d6b71dbc62.png) that is skew symmetric
that is skew symmetric ![\displaystyle [ D,E ] + (-1)^{|D| |E|} [ E,D ] = 0](/images/math/6/c/1/6c1f534b9f85a41f1abe28df4b859fc4.png)
![\displaystyle [D, [ E,F ]] + (-1)^{|D| (|E| + |F|)} [ E, [F,D ]] + (-1)^{|F| (|D| + |E|)} [ F, [ D,E ]] = 0.](/images/math/f/5/9/f595128d405d34d21d951cb31b74b3c6.png)
Note that we cyclically permuted the 3 symbols and put down the signs according to the above sign rule.
2 Super Manifolds
Tex syntax erroris
Tex syntax errorequipped with the sheaf
Tex syntax errorof commutative super
Tex syntax error-algebras
Tex syntax error.
 of dimension
of dimension Tex syntax erroris a pair
Tex syntax errorconsisting of a (Hausdorff and second countable) topological space
Tex syntax errortogether with a sheaf of commutative super
Tex syntax error-algebras
Tex syntax errorthat is locally isomorphic to
Tex syntax error. A morphism
Tex syntax errorbetween super manifolds
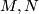 is defined to be a continuous map
is defined to be a continuous map Tex syntax error, together with a map
 of sheaves covering
of sheaves covering Tex syntax error. More precisely, for every open subset
Tex syntax errorthere are algebra maps
Tex syntax error
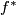 for
for  and we denote this category of super manifolds by
and we denote this category of super manifolds by Tex syntax error.
 there is an associated reduced manifold
there is an associated reduced manifold 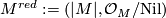
Tex syntax errorand there is an inclusion of super manifolds
Tex syntax error. Note that the sheaf of ideals
Tex syntax erroris generated by odd functions. Other geometric super objects can be defined in a similar way. For example, replacing
Tex syntax errorby
Tex syntax errorand
Tex syntax errorby analytic functions one obtains complex (analytic) super manifolds. There is also an important notion of cs manifolds. These are spaces equipped with sheaves of commutative super
Tex syntax error-algebras that locally look like
Tex syntax error. One relevance of cs manifolds is that they appear naturally as the smooth super manifolds underlying complex analytic super manifolds. In our work, cs manifolds are essential to define the notion of a unitary field theory but this is not relevant for the current discussion.
Example 2.2.
Let be a real vector bundle of fiber dimension
be a real vector bundle of fiber dimension  over the ordinary manifold
over the ordinary manifold Tex syntax errorand
Tex syntax errorthe associated algebra bundle of alternating multilinear forms on
 . Then its sheaf of sections gives a super manifold
. Then its sheaf of sections gives a super manifold Tex syntax errorof dimension
Tex syntax error, denoted by
Tex syntax error. In the current smooth setting, Marjorie Batchelor proved in [Batchelor1979] that every super manifold is isomorphic to one of this type (this is not true for analytic super manifolds). More precisely, let
Tex syntax errordenote the category of real vector bundles over smooth manifolds, and for
Tex syntax error, consider the vector bundle
Tex syntax errorover
Tex syntax errorwith sheaf of sections
Tex syntax error. Then the functors
Tex syntax error
Tex syntax errorbut there are only non-natural isomorphisms
Tex syntax error, coming from a choice of a partition of unity. In other words, these functors induce a bijection on isomorphism classes of objects and inclusions on morphisms but they are not equivalences of categories because there are many more morphims in
Tex syntax errorthan the linear bundle maps coming from
Tex syntax error.
Tex syntax errorfor the algebra of (global) functions on a super manifold
 .
.
Proposition 2.3.
ForTex syntax error, the functor
Tex syntax errorinduces natural bijections
Tex syntax error
Tex syntax erroris an open super submanifold (a
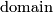 ),
), Tex syntax erroris in bijective correspondence with those
Tex syntax errorin
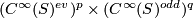 that satisfy
that satisfy
Tex syntax error
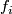 ,
, Tex syntax errorare called the coordinates of
Tex syntax errordefined by
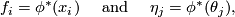
Tex syntax errorare coordinates on
Tex syntax error. Moreover, by the first part we see that
Tex syntax errorand hence
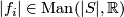 .
.
The proof of the first part is based on the existence of partitions of unity for super manifolds, so it is false in analytic settings. The second part always holds and is proved in [Leites1980].
3 The Functor of Points
 -points, i.e. instead of
-points, i.e. instead of  itself one considers the morphism sets
itself one considers the morphism sets Tex syntax error, where
 varies over all super manifolds
varies over all super manifolds  . More formally, embed the category
. More formally, embed the category Tex syntax errorof super manifolds in the category of contravariant functors from
Tex syntax errorto
Tex syntax errorby
Tex syntax error
Tex syntax errorwith the the category of representable functors, defined to be those in the image of
 . We will sometimes refer to an arbitrary functor
. We will sometimes refer to an arbitrary functor Tex syntax erroras a generalized super manifold. Note that Proposition 2.3 makes it easy to describe the morphism sets
Tex syntax error. We'd also like to point out that the functor of points approach is closely related to computations involving additional odd quantities (the odd coordinates of
 as opposed to those of
as opposed to those of  ) in many physics papers.
) in many physics papers.
4 Super Lie Groups
Tex syntax error. According to the functor of points approach, such a group object in
Tex syntax errorcan be described by giving a functor
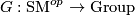 such that the composition with the forgetful functor
such that the composition with the forgetful functor 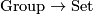 is representable.
is representable.
Example 4.1.
The simplest super Lie group is the additive group structure on 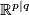 . It is given by the following composition law on
. It is given by the following composition law on 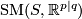 , obviously natural in
, obviously natural in  :
:
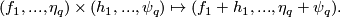
The super general linear group 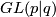 is defined by
is defined by
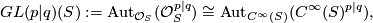
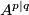 denotes the
denotes the  -module freely generated by
-module freely generated by  even and
even and  odd generators. We need to check that this is representable. We claim that
odd generators. We need to check that this is representable. We claim that 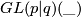 is represented by the open super submanifold
is represented by the open super submanifold 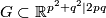 characterized by
characterized by 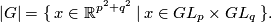
This follows directly from proposition 2.3 using that a map between super algebras is invertible if and only if it is invertible modulo nilpotent elements.
5 Super Vector Bundles
 is a locally free sheaf
is a locally free sheaf 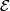 of
of Tex syntax error-modules of dimension
Tex syntax error. The most basic example of a super vector bundle is the tangent bundle of a super manifold
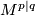 . It is the sheaf of
. It is the sheaf of Tex syntax error-modules
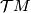 defined by
defined by
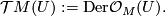
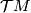 is locally free of dimension
is locally free of dimension Tex syntax error: If
 are local coordinates on
are local coordinates on  , then a local basis is given by
, then a local basis is given by  . Note that there is also a linear fibre bundle
. Note that there is also a linear fibre bundle 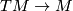 with structure group
with structure group 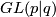 , where
, where  is a super manifold of dimension
is a super manifold of dimension 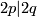 . More generally, any vector bundle
. More generally, any vector bundle 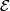 over
over  has a total space
has a total space 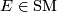 that comes with a projection map
that comes with a projection map 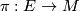 . It can be most easily described in terms of its
. It can be most easily described in terms of its  -points
-points
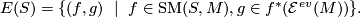
So  is an even global section of the pullback bundle on
is an even global section of the pullback bundle on  and the projection
and the projection  comes from forgetting this datum. To prove that this functor
comes from forgetting this datum. To prove that this functor 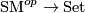 is representable one uses the local triviality of
is representable one uses the local triviality of 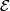 and Proposition 2.3. It follows by construction that the typical fibre of the projection
and Proposition 2.3. It follows by construction that the typical fibre of the projection  is
is 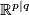 and the structure group is
and the structure group is 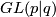 .
.
 . It is an involution
. It is an involution 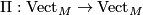
 with grading involution
with grading involution  to
to 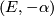 . This means that even and odd parts are exchanged. To define
. This means that even and odd parts are exchanged. To define 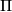 on morphisms it is easiest to give it as
on morphisms it is easiest to give it as 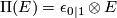 , where
, where 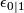 is the trivial bundle of dimension
is the trivial bundle of dimension 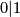 (aka the constant sheaf of free
(aka the constant sheaf of free Tex syntax error-modules).
One can define the super Lie algebra 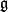 of a super Lie group
of a super Lie group  as follows. A vector field
as follows. A vector field 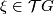 is called left-invariant if
is called left-invariant if  is related to itself under the left-translation by all
is related to itself under the left-translation by all 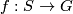 :
:
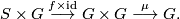
 as a vertical vector field on
as a vertical vector field on 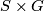 in the obvious way. The super Lie algebra
in the obvious way. The super Lie algebra 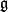 consists of all left-invariant vector fields on
consists of all left-invariant vector fields on  . Pulling back via the unit
. Pulling back via the unit 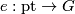 defines an isomorphism
defines an isomorphism 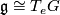 , in particular, the vector space dimension of
, in particular, the vector space dimension of 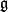 is
is Tex syntax error.
6 Footnotes
- ↑ Whenever we write formulas involving the degree
 of certain elements, we implicitly assume that these elements are homogenous.
of certain elements, we implicitly assume that these elements are homogenous.
7 References
- [Batchelor1979] M. Batchelor, The structure of supermanifolds, Trans. Amer. Math. Soc. 253 (1979), 329–338. MR536951 (80h:58002) Zbl 0413.58002
- [Berezin1987] F. A. Berezin, Introduction to algebra and analysis with anticommuting variables, Reidel 1987.
- [Deligne&Morgan1999] P. Deligne and J. W. Morgan, Notes on supersymmetry (following Joseph Bernstein), Quantum fields and strings: a course for mathematicians, Vol. 1, 2 (Princeton, NJ, 1996/1997), 41–97, Amer. Math. Soc., Providence, RI, (1999), 41–97. MR1701597 (2001g:58007) Zbl 1170.58302
- [Hohnhold&Kreck&Stolz&Teichner2010] H. Hohnhold, M. Kreck, S. Stolz and P. Teichner, Differential Forms and 0-dimensional Super Symmetric Field Theories, to appear in Quantum Topology, Journal of the European Math. Soc. (2010).
- [Leites1980] D. A. Leites, Introduction to the theory of supermanifolds, Russian Math. Surveys 35 No 1 (1980), 3–57. MR0565567 (81j:58003) Zbl 0439.58007
- [Manin1988] Y. I. Manin, Gauge field theory and complex geometry, Springer-Verlag, Berlin, 1988. MR954833 (89d:32001) Zbl 0884.53002
- [Stolz&Teichner2008] S. Stolz and P. Teichner, Supersymmetric Euclidean field theories and generalized cohomology, Survey (2008). Available at http://math.berkeley.edu/~teichner/Papers/Survey.pdf.
- [Voronov1991] T. Voronov, Geometric integration theory on supermanifolds, Harwood Academic Publishers, Chur, 1991. MR1202882 (95b:58023) Zbl 0839.58014
8 External links
- The Wikipedia page on Super manifolds.