Structures on M x I (Ex)
From Manifold Atlas
Revision as of 11:44, 30 May 2012 by Martin Olbermann (Talk | contribs)
Let  be a closed oriented topological manifold of dimension
be a closed oriented topological manifold of dimension  and let
and let
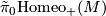 denote the pseudo-isotopy group of orientation preserving self homeomorphisms of
denote the pseudo-isotopy group of orientation preserving self homeomorphisms of  : two self homeomorphisms
: two self homeomorphisms 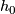 and
and 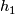 are pseudo-isotopic if they extend to a homeomorphism
are pseudo-isotopic if they extend to a homeomorphism 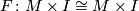 : the group operation is composition. Let
: the group operation is composition. Let
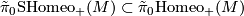
be the subgroup of equivalences classes which are homotopic to the identity.
Exercise 0.1.
Using the fact that the topological surgery exact sequence is a long exact sequence of abelian groups show that  is abelian.
is abelian.