Structures on M x I (Ex)
From Manifold Atlas
(Difference between revisions)
m |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Let $M$ be a closed oriented topological manifold | + | Let $M$ be a closed oriented topological manifold of dimension $n \geq 5$ and let |
| − | $\tilde \pi_0 \textup{Homeo}_+(M)$ denote the pseudo-isotopy group of orientation preserving self homeomorphisms of $M$: two self homeomorphisms $h_0$ and $h_1$ are pseudo- | + | $\tilde \pi_0 \textup{Homeo}_+(M)$ denote the pseudo-isotopy group of orientation preserving self homeomorphisms of $M$: two self homeomorphisms $h_0$ and $h_1$ are pseudo-isotopic if they extend to a homeomorphism $F \colon M \times I \cong M \times I$: the group operation is composition. Let |
$$ \tilde \pi_0 \textup{SHomeo}_+(M) \subset \tilde \pi_0 \textup{Homeo}_+(M) $$ | $$ \tilde \pi_0 \textup{SHomeo}_+(M) \subset \tilde \pi_0 \textup{Homeo}_+(M) $$ | ||
be the subgroup of equivalences classes which are homotopic to the identity. | be the subgroup of equivalences classes which are homotopic to the identity. | ||
| Line 8: | Line 8: | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | |||
| − | |||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| − | [[Category:Exercises | + | [[Category:Exercises with solution]] |
Latest revision as of 12:33, 31 May 2012
Let  be a closed oriented topological manifold of dimension
be a closed oriented topological manifold of dimension 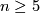 and let
and let
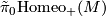 denote the pseudo-isotopy group of orientation preserving self homeomorphisms of
denote the pseudo-isotopy group of orientation preserving self homeomorphisms of  : two self homeomorphisms
: two self homeomorphisms 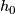 and
and 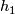 are pseudo-isotopic if they extend to a homeomorphism
are pseudo-isotopic if they extend to a homeomorphism 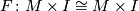 : the group operation is composition. Let
: the group operation is composition. Let
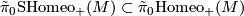
be the subgroup of equivalences classes which are homotopic to the identity.
Exercise 0.1.
Using the fact that the topological surgery exact sequence is a long exact sequence of abelian groups show that  is abelian.
is abelian.