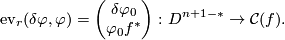Structured chain complexes V (Ex)
From Manifold Atlas
Revision as of 12:19, 25 August 2013 by Tibor Macko (Talk | contribs)
Let 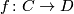 and
and 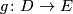 be chain maps and let
be chain maps and let 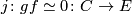 be a chain homotopy from~
be a chain homotopy from~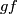 to~
to~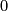 . Then the formula
. Then the formula
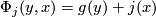
gives another chain map 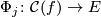 making the following diagram commutative
making the following diagram commutative
![\displaystyle \xymatrix{C \ar[r]^{f} & D \ar[r]^{e} \ar[dr]_{g} & \mathcal{C}(f) \ar@{-->}[d]^{\Phi_j} \\ & & E }](/images/math/3/0/d/30db3c39d5fd27d72f99d239cd753f12.png)
Find appropriate 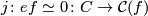 for which we have
for which we have
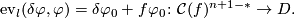
and
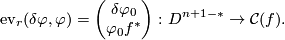
[edit] References
$. Then the formula $$ \Phi_j (y,x) = g(y) + j(x) $$ gives another chain map $\Phi_j \colon \mathcal{C} (f) \rightarrow E$ making the following diagram commutative $$ \xymatrix{C \ar[r]^{f} & D \ar[r]^{e} \ar[dr]_{g} & \mathcal{C}(f) \ar@{-->}[d]^{\Phi_j} \ & & E } $$ Find appropriate $j \colon ef \simeq 0 \colon C \rightarrow \mathcal{C} (f)$ for which we have $$ \mathrm{ev}_l (\delta \varphi,\varphi) = \delta\varphi_0 + f \varphi_0 \colon \mathcal{C} (f)^{n+1-\ast} \rightarrow D. $$ and $$ \mathrm{ev}_r (\delta \varphi,\varphi) = \begin{pmatrix} \delta \varphi_0 \ \varphi_0 f^\ast \end{pmatrix} \colon D^{n+1-\ast} \rightarrow \mathcal{C} (f). $$ == References == {{#RefList:}} [[Category:Exercises]] [[Category:Exercises without solution]]f \colon C \rightarrow D and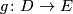 be chain maps and let
be chain maps and let 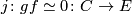 be a chain homotopy from~
be a chain homotopy from~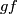 to~
to~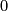 . Then the formula
. Then the formula
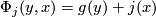
gives another chain map 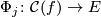 making the following diagram commutative
making the following diagram commutative
![\displaystyle \xymatrix{C \ar[r]^{f} & D \ar[r]^{e} \ar[dr]_{g} & \mathcal{C}(f) \ar@{-->}[d]^{\Phi_j} \\ & & E }](/images/math/3/0/d/30db3c39d5fd27d72f99d239cd753f12.png)
Find appropriate 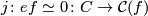 for which we have
for which we have
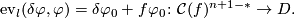
and