Structure set (Ex)
(Difference between revisions)
(Created page with "<wikitex>; ... </wikitex> == References == {{#RefList:}} Category:Exercises Category:Exercises without solution") |
|||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | Let $\mathcal{S} = \{[f:M\simeq N]\}$ be the structure set of a closed manifold and let $\mathcal{E}(M)$ be the group of homotopy self-equivalences of $M$. Note that $\mathcal{E}(M)$ acts on $\mathcal{S}(M)$ by post composition: $$ \begin{array}{rcl} \mathcal{S}(M) \times \mathcal{E}(M) & \to & \mathcal{S}(M),\\ ([f:N\to M],[g]) &\mapsto& [g\circ f: N\to M].\end{array}$$ Show that the set $\mathcal{M}(M):= \mathcal{S}(M)/\mathcal{E}(M)$ is in bijection with the set of diffeomorphism classes of manifolds homotopy equivalent to $M$. |
</wikitex> | </wikitex> | ||
== References == | == References == | ||
Revision as of 21:12, 25 August 2013
![\mathcal{S} = \{[f:M\simeq N]\}](/images/math/8/1/f/81fc9a013fae667d9de253e482366df5.png) be the structure set of a closed manifold and let
be the structure set of a closed manifold and let 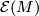 be the group of homotopy self-equivalences of
be the group of homotopy self-equivalences of  . Note that
. Note that 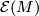 acts on
acts on 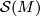 by post composition:
by post composition: ![\displaystyle \begin{array}{rcl} \mathcal{S}(M) \times \mathcal{E}(M) & \to & \mathcal{S}(M),\\ ([f:N\to M],[g]) &\mapsto& [g\circ f: N\to M].\end{array}](/images/math/6/9/2/6922b84f7fc78f50d4a99628008d9f22.png)
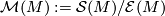 is in bijection with the set of diffeomorphism classes of manifolds homotopy equivalent to
is in bijection with the set of diffeomorphism classes of manifolds homotopy equivalent to  .
.