String bordism
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
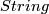 -bordism or
-bordism or 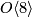 -bordism is a special case of a B-bordism. It comes from the tower of fibrations below.
-bordism is a special case of a B-bordism. It comes from the tower of fibrations below.
![\displaystyle \xymatrix{BO\!\left< 8 \right>\ar[d] & \\ BSpin \ar[d]\ar[r]^{p_1/2}&K({\mathbb Z},4) \\ BSO\ar[d]\ar[r]^{w_2}& K({\mathbb Z}/2,2) \\ BO\ar[r]^{w_1}& K({\mathbb Z}/2,1) }](/images/math/3/7/b/37bd1f92c9a30f2b9da4996d3a8aa181.png)
In each step the lowest homotopy group is killed by the map into the Eilenberg-MacLane spaces. In particular, 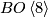 is the homotopy fibre of the map from
is the homotopy fibre of the map from 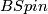 given by half of the first Pontryagin class. The name
given by half of the first Pontryagin class. The name 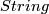 -group is due to Haynes Miller and will be explained below.
-group is due to Haynes Miller and will be explained below.
2 The String group
There are various models for the String group. However, since its first three homotopy groups vanish it can not be realized as a finite dimensional Lie group. There are homotopy theoretic constructions which involve path spaces. A more geometric way to think about 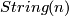 which involves only finite dimensional manifolds is the following: the String group fibers over the Spin group with fibre
which involves only finite dimensional manifolds is the following: the String group fibers over the Spin group with fibre 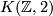 . One may think of
. One may think of 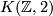 as the realization of
as the realization of  viewed as a smooth category with only one object. This way, the
viewed as a smooth category with only one object. This way, the 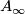 space
space 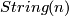 appears as the realization of a smooth 2-group extension of
appears as the realization of a smooth 2-group extension of  by the finite dimensional Lie groupoid
by the finite dimensional Lie groupoid  (see [Schommer-Pries2009]). A more explicit model for this extension can be found in [Meinrenken2003].
(see [Schommer-Pries2009]). A more explicit model for this extension can be found in [Meinrenken2003].
3 The bordism groups
The additive structure of the bordism groups is not fully determined yet. It is known that only 2 and 3 torsion appears (see [Giambalvo1971]) and the 3 torsion is annihalated by multiplication with 3 (see [Hovey1997]). Moreover, the bordism groups 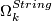 are finite for
are finite for 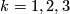 mod 4.
mod 4.
Clearly, since 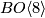 is 7-connected the first 6 bordism groups coincide with the framed bordism groups. The first 16 bordism groups have been computed by Giambalvo [Giambalvo1971, p. 538]:
is 7-connected the first 6 bordism groups coincide with the framed bordism groups. The first 16 bordism groups have been computed by Giambalvo [Giambalvo1971, p. 538]:
-
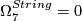 .
.
-
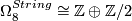 , generated by the exotic 8-sphere for the 2-torsion and a certain Bott manifold: see [Laures2004].
, generated by the exotic 8-sphere for the 2-torsion and a certain Bott manifold: see [Laures2004].
-
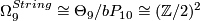 , generated by exotic 9-spheres.
, generated by exotic 9-spheres.
-
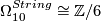 , generated by an exotic 10-sphere.
, generated by an exotic 10-sphere.
-
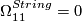 .
.
-
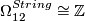 , generated by a 5-connected manifold with signature
, generated by a 5-connected manifold with signature 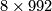 .
.
-
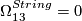 .
.
-
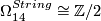 , generated by the exotic 14-sphere.
, generated by the exotic 14-sphere.
-
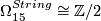 , genreated by the exotic 15-sphere.
, genreated by the exotic 15-sphere.
-
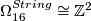 .
.
At the prime 3 the first 32 bordism groups can be found in [Hovey&Ravenel1995]. Further calculations have been done in [Mahowald&Gorbounov1995].
4 Homology calculations
4.1 Singular homology
The cohomology ring 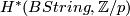 has been computed for
has been computed for 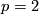 by Stong in [Stong1963]:
by Stong in [Stong1963]:
![\displaystyle H^*(BString)\cong {\mathbb Z}/2[\theta_i|\sigma_2(i+1)>4]\otimes H^*(K({\mathbb Z},4))/Sq^2(\iota).](/images/math/1/6/6/1664d6ce54e6548005e8bdcb8febb4bb.png)
Here, 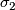 is the number of digits in the duadic decomposition and the
is the number of digits in the duadic decomposition and the 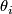 come from the cohomology of
come from the cohomology of 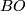 and coincide with the Stiefel-Whitney up to decomposables. For odd
and coincide with the Stiefel-Whitney up to decomposables. For odd  the corresponding result has been obtained by Giambalvo [Giambalvo1969].
the corresponding result has been obtained by Giambalvo [Giambalvo1969].
4.2 K(1)-local computations
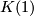 locally
locally 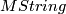 coincides with
coincides with 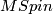 and decomposes into a wedge of copies of
and decomposes into a wedge of copies of  . However, it is not an algebra over
. However, it is not an algebra over  . Its multiplicative structure for
. Its multiplicative structure for 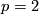 can be read off the formula
can be read off the formula
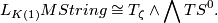
Here, 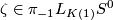 is a generator,
is a generator, 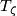 is the
is the 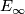 cone over
cone over 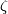 and
and 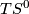 is the free
is the free 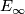 spectrum generated by the sphere. In particular, its
spectrum generated by the sphere. In particular, its 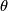 -algebra structure is free (see [Laures2003a]).
-algebra structure is free (see [Laures2003a]).
4.3 K(n)-local computations
For 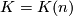 at
at 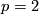 one has an exact sequence of Hopf algebras (see [Kitchloo&Laures&Wilson2004a])
one has an exact sequence of Hopf algebras (see [Kitchloo&Laures&Wilson2004a])
![\displaystyle \xymatrix{K_* \ar[r] & K_*K({\mathbb Z}/2,2)\ar[r]& K_*K({\mathbb Z},3)\ar[r]& K_*BString \ar[r]&K_*BSpin \ar[r]& K_* K({\mathbb Z},4)\ar[r]^2& K({\mathbb Z},4)\ar[r]&K_*}](/images/math/a/e/c/aec9eeebe1b3ea17211973d679e21b2b.png)
which is induced by the obvious geometric maps. For  it algebraically reduces to the split exact sequence of Hopf algebras (see [Kitchloo&Laures&Wilson2004b])
it algebraically reduces to the split exact sequence of Hopf algebras (see [Kitchloo&Laures&Wilson2004b])
![\displaystyle \xymatrix{K(2)_* \ar[r] & K(2)_*K({\mathbb Z},3)\ar[r]& K(2)_*BString \ar[r]&K(2)_*BSpin \ar[r]& K(2)_*}.](/images/math/8/d/3/8d3e325bb23de7bca738ff651bce7d49.png)
4.4 Computations with respect to general complex oriented theories
Ando, Hopkins and Strickland investigated the homology ring 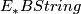 for even periodic multiplicative cohomology theories
for even periodic multiplicative cohomology theories  . Even periodic theories are complex orientable which means that
. Even periodic theories are complex orientable which means that 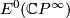 carries a formal group. The description of
carries a formal group. The description of 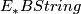 is in terms of formal group data.
is in terms of formal group data.
In [Ando&Hopkins&Strickland2001a] first the analogous complex problem is studied. The group 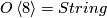 has a complex relative
has a complex relative 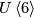 which is defined in the same way by killing the third homotopy group of
which is defined in the same way by killing the third homotopy group of 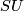 . Consider the map
. Consider the map
![\displaystyle (1-L_1)(1-L_2)(1-L_3): \xymatrix{ {\mathbb C}P^\infty \times {\mathbb C}P^\infty\times {\mathbb C}P^\infty\ar[r]& BU}](/images/math/2/f/a/2fac94ccd29b1dc79cae94b3be9d5e92.png)
where the 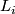 are the canonical line bundles over the individual factors. Since the first two Chern classes of the virtual bundle vanish the map lifts to
are the canonical line bundles over the individual factors. Since the first two Chern classes of the virtual bundle vanish the map lifts to 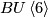 . If we choose a complex orienatation the lift gives a class
. If we choose a complex orienatation the lift gives a class  in the cohomology
ring
in the cohomology
ring
![\displaystyle (E\wedge BU\left<6 \right>_+)^0( {\mathbb C}P^\infty \times {\mathbb C}P^\infty\times {\mathbb C}P^\infty )\cong E_0BU\left<6 \right> [\![x_1,x_2,x_3]\!]](/images/math/d/c/4/dc4cb9d322190b22fc956cc8c14e17ee.png)
with 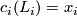 . The power series
. The power series  satisfies the following identities:
satisfies the following identities:
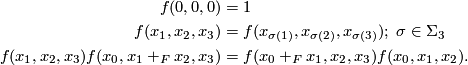
Hence, the power series is an example a symmetric 3-cocycle or a cubical structure on the formal group law. In fact the main result of [Ando&Hopkins&Strickland2001a] is that it is the universal example of such a structure. Explicitly, this means that the commutative ring 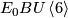 is freely generated by the coefficients of
is freely generated by the coefficients of  subject to the relations given by the 3 equations above.
subject to the relations given by the 3 equations above.
The real version of this result has not been published yet by the three authors. Using the diagram
![\displaystyle \xymatrix{K{\mathbb Z},3)\ar[r]\ar[d]^=&BU\left< 6 \right>\ar[r]\ar[d]& BSU\ar[d]\\ K({\mathbb Z},3)\ar[r]& BString \ar[r]&BSpin}](/images/math/a/c/5/ac57f74e455c2ea2a8226749edfe4703.png)
and the results for 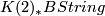 described above they conjecture that
described above they conjecture that 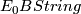 is the same quotient subject to the additional relation
is the same quotient subject to the additional relation
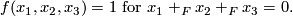
5 The structure of the spectrum
Localized at a prime 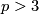 , string bordism splits additively into a sum of suspensions of
, string bordism splits additively into a sum of suspensions of 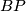 , although the ring structure is different (see [Hovey2008]). For
, although the ring structure is different (see [Hovey2008]). For 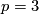 there is a spectrum
there is a spectrum  with 3 cells in even dimensions such that
with 3 cells in even dimensions such that 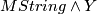 splits into a sum of suspensions of
splits into a sum of suspensions of 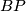 . For
. For 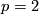 it is hoped that the spectrum
it is hoped that the spectrum 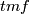 splits off which is explained below.
splits off which is explained below.
6 The Witten genus
At the end of the 80s Ed Witten were studying the  -equivariant index of the Dirac operator on a loop space of a
-equivariant index of the Dirac operator on a loop space of a  -dimensional manifold. For compact manifolds a Dirac operator exists if the manifold is Spin. For the loop space
-dimensional manifold. For compact manifolds a Dirac operator exists if the manifold is Spin. For the loop space 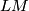 this would mean that
this would mean that  is
is 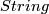 . Witten carried the Atiyah-Segal formula for the index over to this infinite dimensional setting and obtained an integral modular form of weight
. Witten carried the Atiyah-Segal formula for the index over to this infinite dimensional setting and obtained an integral modular form of weight  . Nowadays this is called the Witten genus (see [Segal1988].)
The Witten genus can be refined to a map of structured ring spectra
. Nowadays this is called the Witten genus (see [Segal1988].)
The Witten genus can be refined to a map of structured ring spectra
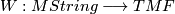
from the Thom spectrum of String bordism to the spectrum 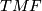 of topological modular forms ([Hopkins2002]). This map is also called the
of topological modular forms ([Hopkins2002]). This map is also called the 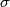 -orientation and is 15-connected (see [Hill2008]). The spectrum
-orientation and is 15-connected (see [Hill2008]). The spectrum 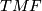 was developed by Goerss, Hopkins and Miller. It is supposed to play the same role for
was developed by Goerss, Hopkins and Miller. It is supposed to play the same role for 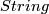 -bordism as
-bordism as  -theory does for
-theory does for 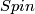 -bordism. Its coefficients localized away from 2 and 3 are given by the integral modular forms. The map
-bordism. Its coefficients localized away from 2 and 3 are given by the integral modular forms. The map  gives characteristic numbers which together with
gives characteristic numbers which together with  and Stiefel-Whitney numbers are conjectured to determine the
and Stiefel-Whitney numbers are conjectured to determine the 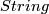 bordism class. Moreover,
bordism class. Moreover, 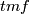 is supposed to be a direct summand of
is supposed to be a direct summand of 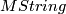 as the orientation map
as the orientation map  is shown to be surjective in homotopy (see [Hopkins&Mahowald2002].)
is shown to be surjective in homotopy (see [Hopkins&Mahowald2002].)
7 References
- [Ando&Hopkins&Strickland2001a] M. Ando, M. J. Hopkins and N. P. Strickland, Elliptic spectra, the Witten genus and the theorem of the cube, Invent. Math. 146 (2001), no.3, 595–687. MR1869850 (2002g:55009) Zbl 1031.55005
- [Giambalvo1969] V. Giambalvo, The
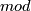
 cohomology of
cohomology of 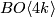 , Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
, Proc. Amer. Math. Soc. 20 (1969), 593–597. MR0236913 (38 #5206) Zbl 0176.52601
- [Giambalvo1971] V. Giambalvo, On
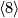 -cobordism, Illinois J. Math. 15 (1971), 533–541. MR0287553 (44 #4757) Zbl 0221.57019
-cobordism, Illinois J. Math. 15 (1971), 533–541. MR0287553 (44 #4757) Zbl 0221.57019
- [Hill2008] M. A. Hill, The String bordism of
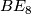 and
and 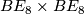 through dimension 14, (2008). Available at the arXiv:arXiv:0807.2095v1.
through dimension 14, (2008). Available at the arXiv:arXiv:0807.2095v1.
- [Hopkins&Mahowald2002] M. Mahowald and M. Hopkins, The structure of 24 dimensional manifolds having normal bundles which lift to
![BO[8]](/images/math/f/d/a/fdac308686775b92582a7ae9ef0116f3.png) , Recent progress in homotopy theory (Baltimore, MD, 2000), Contemp. Math., 293 (2002), 89–110. MR1887530 (2003b:55007) Zbl 1012.57041
, Recent progress in homotopy theory (Baltimore, MD, 2000), Contemp. Math., 293 (2002), 89–110. MR1887530 (2003b:55007) Zbl 1012.57041
- [Hopkins2002] M. J. Hopkins, Algebraic topology and modular forms, (2002), 291–317. MR1989190 (2004g:11032) Zbl 1031.55007
- [Hovey&Ravenel1995] M. A. Hovey and D. C. Ravenel, The
 -connected cobordism ring at
-connected cobordism ring at 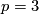 , Trans. Amer. Math. Soc. 347 (1995), no.9, 3473–3502. MR1297530 (95m:55008) Zbl 0852.55008
, Trans. Amer. Math. Soc. 347 (1995), no.9, 3473–3502. MR1297530 (95m:55008) Zbl 0852.55008
- [Hovey1997] M. A. Hovey,
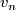 -elements in ring spectra and applications to bordism theory, Duke Math. J. 88 (1997), no.2, 327–356. MR1455523 (98d:55017) Zbl 0880.55006
-elements in ring spectra and applications to bordism theory, Duke Math. J. 88 (1997), no.2, 327–356. MR1455523 (98d:55017) Zbl 0880.55006
- [Hovey2008] M. Hovey, The homotopy of
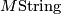 and
and 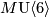 at large primes, Algebr. Geom. Topol. 8 (2008), no.4, 2401–2414. MR2465746 (2009h:55002) Zbl 1165.55001
at large primes, Algebr. Geom. Topol. 8 (2008), no.4, 2401–2414. MR2465746 (2009h:55002) Zbl 1165.55001
- [Kitchloo&Laures&Wilson2004a] N. Kitchloo, G. Laures and W. S. Wilson, The Morava
 -theory of spaces related to
-theory of spaces related to 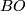 , Adv. Math. 189 (2004), no.1, 192–236. MR2093483 (2005k:55002) Zbl 1063.55002
, Adv. Math. 189 (2004), no.1, 192–236. MR2093483 (2005k:55002) Zbl 1063.55002
- [Kitchloo&Laures&Wilson2004b] N. Kitchloo, G. Laures and W. S. Wilson, Splittings of bicommutative Hopf algebras, J. Pure Appl. Algebra 194 (2004), no.1-2, 159–168. MR2086079 (2005e:55019) Zbl 1066.16041
- [Laures2003a] G. Laures, An
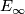 splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
- [Laures2004] G. Laures,
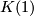 -local topological modular forms, Invent. Math. 157 (2004), no.2, 371–403. MR2076927 (2005h:55003) Zbl 1078.55010
-local topological modular forms, Invent. Math. 157 (2004), no.2, 371–403. MR2076927 (2005h:55003) Zbl 1078.55010
- [Mahowald&Gorbounov1995] M. Mahowald and V. Gorbounov, Some homotopy of the cobordism spectrum
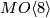 , Homotopy theory and its applications (Cocoyoc, 1993), Amer. Math. Soc. (1995), 105–119. MR1349133 (96i:55010) Zbl 0840.55002
, Homotopy theory and its applications (Cocoyoc, 1993), Amer. Math. Soc. (1995), 105–119. MR1349133 (96i:55010) Zbl 0840.55002
- [Meinrenken2003] E. Meinrenken, The basic gerbe over a compact simple Lie group, Enseign. Math. (2) 49 (2003), no.3-4, 307–333. MR2026898 (2004j:53064) Zbl 1061.53034
- [Schommer-Pries2009] C. Schommer-Pries, Central Extensions of Smooth 2-Groups and a Finite-Dimensional String 2-Group, (2009). Available at the arXiv:0911.2483.
- [Segal1988] G. Segal, Elliptic cohomology (after Landweber-Stong, Ochanine, Witten, and others), Séminaire Bourbaki, Vol. 1987/88, Astérisque No. 161-162 (1988), Exp. No. 695, 4, (1989) 187–201. MR992209 (91b:55005) Zbl 0686.55003
- [Stong1963] R. E. Stong, Determination of
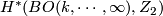 and
and 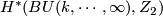 , Trans. Amer. Math. Soc. 107 (1963), 526–544. MR0151963 (27 #1944) Zbl 0116.14702
, Trans. Amer. Math. Soc. 107 (1963), 526–544. MR0151963 (27 #1944) Zbl 0116.14702