Stiefel-Whitney characteristic classes
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a compact smooth
be a compact smooth  -manifold (possibly with boundary).
Denote by
-manifold (possibly with boundary).
Denote by 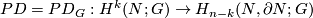 the Poincaré duality isomorphism.
Here for non-orientable
the Poincaré duality isomorphism.
Here for non-orientable  the coefficients in cohomology are twisted (by the orientation double covering) and the coefficients in homology are non-twisted.
Let
the coefficients in cohomology are twisted (by the orientation double covering) and the coefficients in homology are non-twisted.
Let 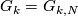 be
be  if either
if either 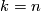 or
or 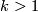 is odd, and
is odd, and  if either
if either 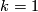 or
or  is even.
is even.
Stiefel defined the homology Stiefel-Whitney class 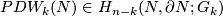 of
of  to be the homology class of a degeneracy subset of a general position collection of
to be the homology class of a degeneracy subset of a general position collection of 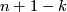 tangent vector fields on
tangent vector fields on  . Let
. Let 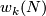 be the reduction of
be the reduction of 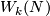 modulo 2.
modulo 2.
Whitney defined the homology normal Stiefel-Whitney class 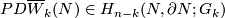 of
of  to be the homology class of a degeneracy subset of a general position collection of
to be the homology class of a degeneracy subset of a general position collection of 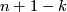 normal vector fields on
normal vector fields on  . Let
. Let 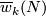 be the reduction of
be the reduction of 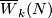 modulo 2.
modulo 2.
See details e.g. in [Milnor&Stasheff1974,  12], [Fomenko&Fuchs2016,
12], [Fomenko&Fuchs2016,  19.C], [Skopenkov2015b,
19.C], [Skopenkov2015b,  9,11,12].
9,11,12].
There is an alternative definition of 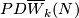 [Skopenkov2006,
[Skopenkov2006,  2.3 `the Whitney obstruction'] analogous to definition of the Whitney invariant.
2.3 `the Whitney obstruction'] analogous to definition of the Whitney invariant.
See also Wikipedia article.
2 References
- [Fomenko&Fuchs2016] A. T. Fomenko and D. B. Fuks, Homotopical Topology. Translated from the Russian. Graduate Texts in Mathematics, 273. Springer-Verlag, Berlin, 2016. DOI 10.1007/978-3-319-23488-5.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2015b] A. Skopenkov, Algebraic Topology From Geometric Viewpoint (in Russian), MCCME, Moscow, 2015, 2020. Accepted for English translation by `Moscow Lecture Notes' series of Springer. Preprint of a part