Stable classification of 4-manifolds
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
In this page we report about the stable classification of  -manifolds.
-manifolds.
2 Construction and examples
We begin with the construction of manifolds which give many stable diffeomorphism types of  -manifolds:
-manifolds:
-
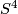
-
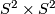
-
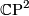
-
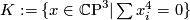 , the Kummer surface.
, the Kummer surface.
Let 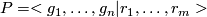 be the presentation of a group
be the presentation of a group  . Then we build a
. Then we build a  -dimensional complex
-dimensional complex 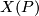 by taking a wedge of
by taking a wedge of  circles and attaching a
circles and attaching a  -cell via each relation
-cell via each relation 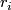 . Then we thicken
. Then we thicken 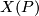 to a smooth compact manifold with boundary
to a smooth compact manifold with boundary 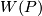 in
in 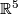 and consider its boundary denoted by
and consider its boundary denoted by 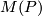 . For details and why this is well defined see Thickenings.
. For details and why this is well defined see Thickenings. 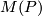 is a smooth
is a smooth  -manifold with fundamental group
-manifold with fundamental group  and we add it to our list
and we add it to our list
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...