Splitting invariants (Ex)
From Manifold Atlas
Revision as of 14:22, 23 March 2012 by Marek Kaluba (Talk | contribs)
Prove that two maps 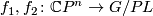 are
homotopic iff their splitting invariants agree for
are
homotopic iff their splitting invariants agree for 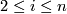 .
.
Use the exact sequence
![\displaystyle L_{2k}(\mathbb{Z}) \to [\mathbb{C}P^k,G/PL] \to [\mathbb{C}P^{k-1},G/PL] \to 0](/images/math/6/a/9/6a91b8ae34455f5fcf5e4d3774192247.png)
![\displaystyle \theta \colon [\mathbb{C}P^k, G/PL] \to L_{2k}(\mathbb{Z})](/images/math/0/1/6/01613f37724925f8fa94f2ff1958dd3e.png)
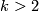 . Additionally
. Additionally ![[\mathbb{C}P^2,G/PL]=\mathbb{Z}](/images/math/9/3/d/93d436989e8b20ba602ee464535fc78a.png) and the isomorphism is given by the surgery obstruction map.
and the isomorphism is given by the surgery obstruction map.