Spin bordism
(→Further topics) |
m (→Rohlin's theorem) |
||
| Line 122: | Line 122: | ||
<wikitex>; | <wikitex>; | ||
Above we stated that the 4-dimensional spin bordism group $\Omega_4^{Spin} \cong \Z$ is generated | Above we stated that the 4-dimensional spin bordism group $\Omega_4^{Spin} \cong \Z$ is generated | ||
| − | by the Kummer surface $K3$ which has signature 16. Consequently we have the following important theorem of | + | by the Kummer surface $K3$ which has signature 16. Consequently we have the following important theorem of Rohlin (which of course was used in calculation of $\Omega_4^{Spin}$ give above). |
{{beginthm|Theorem|\cite{Rohlin1952}}} | {{beginthm|Theorem|\cite{Rohlin1952}}} | ||
The signature of every closed smooth spin $4$-manifold is divisible by $16$. | The signature of every closed smooth spin $4$-manifold is divisible by $16$. | ||
Latest revision as of 08:17, 3 February 2021
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
By the Pontrjagin-Thom isomorphism the spin bordism groups 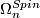 of closed manifolds with spin structures are isomorphic to the homotopy groups of the Thom spectrum
of closed manifolds with spin structures are isomorphic to the homotopy groups of the Thom spectrum 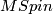 .
.
Preliminary results were by Novikov. The main calculation was achieved in [Anderson&Brown&Peterson1966] and [Anderson&Brown&Peterson1967].
[edit] 2 Invariants
The spin bordism class of a manifold is detected by  -cohomology (Stiefel-Whitney) and KO-theory (Pontryagin) characteristic numbers.
-cohomology (Stiefel-Whitney) and KO-theory (Pontryagin) characteristic numbers.
For a multi-index 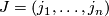 , we set
, we set 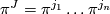 and
and 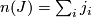 .
.
 -manifold
-manifold  induces a KO-orientation
induces a KO-orientation ![[M]\in KO_n(M)](/images/math/4/0/1/401c80af9787cadfd50c483e0a4e3289.png) , so that we can evaluate polynomials in the KO-Pontryagin classes
, so that we can evaluate polynomials in the KO-Pontryagin classes 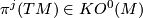 to get characteristic numbers
to get characteristic numbers ![\displaystyle \pi^J(M)=\langle \pi^J(TM), [M] \rangle \in KO_n(pt).](/images/math/e/f/1/ef11fdaca6fe169cbb99a2a7b7bc5cb1.png)
There is an interpretation of these characteristic numbers using index theory:
A feature of Spin manifolds  is that they possess Dirac operators,
is that they possess Dirac operators, 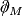 . The (Clifford-linear) Dirac operator can be considered as a representative of the fundamental class
. The (Clifford-linear) Dirac operator can be considered as a representative of the fundamental class ![[M]\in KO_n(M)](/images/math/4/0/1/401c80af9787cadfd50c483e0a4e3289.png) ,
see [Atiyah1970] and [Higson&Roe2000].
The characteristic numbers above can then be defined as the indices of the (Clifford-linear) Dirac operators obtained by twisting with the corresponding vector bundles.
The easiest case is the non-twisted one:
,
see [Atiyah1970] and [Higson&Roe2000].
The characteristic numbers above can then be defined as the indices of the (Clifford-linear) Dirac operators obtained by twisting with the corresponding vector bundles.
The easiest case is the non-twisted one: 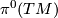 is the trivial bundle, and taking the index of the Dirac operator
is the trivial bundle, and taking the index of the Dirac operator 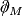 defines an element of
defines an element of 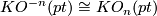 when
when  is n-dimensional. This gives rises to a ring homomorphism often called the
is n-dimensional. This gives rises to a ring homomorphism often called the  -invariant:
-invariant:
![\displaystyle \alpha : \Omega_*^{Spin} \longrightarrow KO_*, ~~~ [M] \longmapsto [\operatorname{ind} \partial\!\!\!/_M]=\alpha(M)=\pi^0(M).](/images/math/5/b/e/5befb82949e3197c345ca4ce92f695f5.png)
See [Lawson&Michelsohn1989].
For  divisible by 4, this invariant equals (up to a factor of 1/2 in dimensions congruent to 4 modulo 8) the
divisible by 4, this invariant equals (up to a factor of 1/2 in dimensions congruent to 4 modulo 8) the 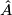 -genus of
-genus of  .
.
[edit] 3 Classification
[edit] 3.1 MSpin away from the prime 2 and at the prime 2
After inverting 2 the map of Thom spectra 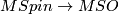 becomes a homotopy equivalence.
becomes a homotopy equivalence.
Using the Thom isomorphism 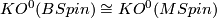 we get for each multi-index
we get for each multi-index 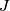 with
with 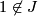 a map
a map 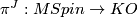 ,
which induces on homotopy groups the map
,
which induces on homotopy groups the map 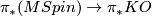 ,
, ![[M]\mapsto \pi^J(M)](/images/math/b/0/1/b01e5922e29db88139d86a642b5ef011.png) described above.
Anderson,Brown and Peterson show that
described above.
Anderson,Brown and Peterson show that 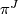 factorizes through
factorizes through 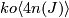 if
if  is even
and
is even
and 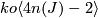 if
if  is odd. Hence the corresponding characteristic numbers vanish
for manifolds of smaller dimension.
is odd. Hence the corresponding characteristic numbers vanish
for manifolds of smaller dimension.
Similarly a Stiefel-Whitney class in 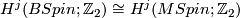 corresponds to a spectrum map
corresponds to a spectrum map 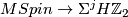 .
.
Theorem 3.1 [Anderson&Brown&Peterson1967].
There are classes 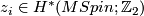 such that there is a 2-local homotopy equivalence
such that there is a 2-local homotopy equivalence
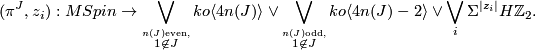
[Anderson&Brown&Peterson1966] also determine the Poincaré polynomial of 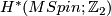 which allows to compute inductively
the degrees
which allows to compute inductively
the degrees 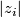 . The first
. The first 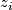 occurs in dimension
occurs in dimension 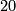 , and there are
, and there are 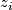 in all dimensions
in all dimensions 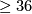 .
.
[edit] 3.2 Consequences
From this one can compute the additive structure of the spin bordism groups completely.
We get a contribution from each 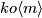 which is 0 below dimension
which is 0 below dimension  , and periodic of period 8 starting from dimension
, and periodic of period 8 starting from dimension  , with values
, with values
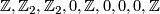 (here the first value corresponds to dimensions congruent to 0 modulo 8).
The contribution from
(here the first value corresponds to dimensions congruent to 0 modulo 8).
The contribution from 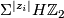 is a single
is a single  in dimension
in dimension 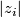 .
.
All  summands are in degrees divisible by 4, and there is no odd torsion in the spin cobordism groups.
All even torsion is of exponent 2, being of two types: that arising by products with a framed
summands are in degrees divisible by 4, and there is no odd torsion in the spin cobordism groups.
All even torsion is of exponent 2, being of two types: that arising by products with a framed  and that which maps monomorphically into unoriented cobordism.
and that which maps monomorphically into unoriented cobordism.
[edit] 3.3 Ring structure
Concerning the multiplicative structure, 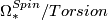 is the subring of an integral polynomial ring on classes
is the subring of an integral polynomial ring on classes 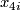 (dimension 4i)
consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8 [Stong1968].
Anderson, Brown and Peterson determine the structure of
(dimension 4i)
consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8 [Stong1968].
Anderson, Brown and Peterson determine the structure of 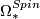 modulo
the ideal consisting of torsion mapping monomorphically into unoriented cobordism.
According to [Laures2003], the multiplicative structure of this ideal is still not completely known.
modulo
the ideal consisting of torsion mapping monomorphically into unoriented cobordism.
According to [Laures2003], the multiplicative structure of this ideal is still not completely known.
[edit] 4 Generators
[edit] 4.1 Low dimensions
The spin bordism groups up to dimension  are given in [Milnor1963a] without proof.
Milnor states that this is the result of a formibable calculation of
are given in [Milnor1963a] without proof.
Milnor states that this is the result of a formibable calculation of 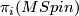 for
for 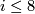 .
.
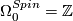 , generated by a point.
, generated by a point.
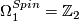 , generated by
, generated by 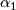 , the circle
with the "antiperiodic" spin structure.
, the circle
with the "antiperiodic" spin structure.
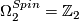 , generated by
, generated by 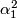 .
.
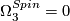 .
.
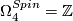 , generated by
, generated by 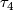 , the Kummer surface.
, the Kummer surface.
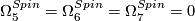 .
.
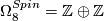 , generated by quaternionic projective space and a generator
, generated by quaternionic projective space and a generator 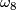 which equals 1/4 of the square of the Kummer surface.
which equals 1/4 of the square of the Kummer surface.
[edit] 4.2 Generators in all dimensions as given by the classification
By the theorem of Anderson, Brown and Peterson there exist manifolds
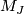 of dimension
of dimension 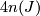 if
if  is even,
is even,
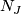 of dimension
of dimension 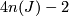 if
if  is odd, and
is odd, and 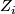 of dimension
of dimension 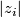 ,
such that the characteristic numbers
,
such that the characteristic numbers 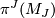 ,
, 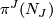 and
and 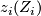 are odd.
For
are odd.
For  odd, let
odd, let 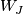 be a spin nullbordism of
be a spin nullbordism of 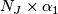 , and let
, and let
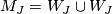 (using an orientation-reversing automorphism of
(using an orientation-reversing automorphism of  ). By [Stong1966] there exist manifolds
). By [Stong1966] there exist manifolds 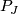 such that
such that
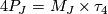 . If all
. If all 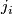 are even,
one can choose
are even,
one can choose 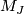 to be a product of quaternionic projective spaces.
to be a product of quaternionic projective spaces.
Then a basis for 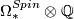 is given by
is given by
-
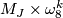 for
for 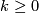
-
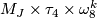 for
for 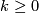 .
.
A basis for 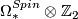 is given by
is given by
-
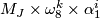 with
with 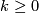 ,
, 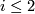 and
and  even,
even,
-
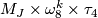 with
with 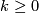 ,
,  even,
even,
-
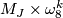 with
with 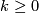 ,
,  odd,
odd,
-
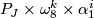 with
with 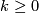 ,
, 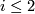 and
and  odd
odd
-
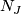 with
with  odd,
odd,
-
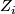 .
.
[edit] 5 Further topics
[edit] 5.1 Rohlin's theorem
Above we stated that the 4-dimensional spin bordism group 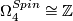 is generated
by the Kummer surface
is generated
by the Kummer surface 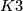 which has signature 16. Consequently we have the following important theorem of Rohlin (which of course was used in calculation of
which has signature 16. Consequently we have the following important theorem of Rohlin (which of course was used in calculation of 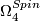 give above).
give above).
Theorem 5.1 [Rohlin1952].
The signature of every closed smooth spin  -manifold is divisible by
-manifold is divisible by 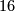 .
.
[edit] 5.2 Relationship with other bordism groups
- Framed bordism: the image of
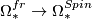 is 0 unless
is 0 unless 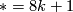 or
or 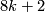 when it is
when it is  and detected by the
and detected by the  -invariant. Explicit generators are
-invariant. Explicit generators are 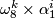 with
with 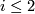 and
and 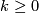 .
.
- Oriented bordism: the kernel of
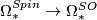 lies in dimensions
lies in dimensions 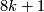 and
and 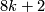 . It is a
. It is a  vector space with a basis
vector space with a basis 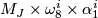 , for
, for  even, and
even, and 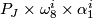 , for
, for  odd, where
odd, where 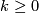 and
and 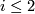 . It is also the ideal generated by the non-trivial class of
. It is also the ideal generated by the non-trivial class of 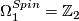 . The cokernel is a finite
. The cokernel is a finite  -torsion group which is trivial if and only if
-torsion group which is trivial if and only if 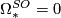 or equivalently
or equivalently 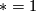 ,
,  ,
,  ,
,  , and
, and  . [Milnor1965] computed
. [Milnor1965] computed 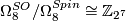 .
.
- Unoriented bordism: the image of
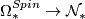 is all bordism classes for which the characteristic numbers divisible by
is all bordism classes for which the characteristic numbers divisible by 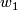 and
and 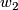 are zero. A basis for the image consists of the
are zero. A basis for the image consists of the 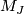 , for
, for  even, the
even, the 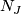 , for
, for  odd and the
odd and the 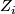 . The image is trivial for
. The image is trivial for  . In even dimensions it is additionally trivial for
. In even dimensions it is additionally trivial for 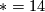 and
and 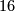 . In odd dimensions it is trivial for
. In odd dimensions it is trivial for 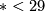 and also for
and also for 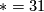 and
and 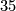 . Otherwise the image is non trivial.
. Otherwise the image is non trivial.
[edit] 6 References
- [Anderson&Brown&Peterson1966] D. W. Anderson, E. H. Brown and F. P. Peterson, Spin cobordism, Bull. Amer. Math. Soc. 72 (1966), 256–260. MR0190939 (32 #8349) Zbl 0156.21605
- [Anderson&Brown&Peterson1967] D. W. Anderson, E. H. Brown and F. P. Peterson, The structure of the Spin cobordism ring, Ann. of Math. (2) 86 (1967), 271–298. MR0219077 (36 #2160) Zbl 0156.21605
- [Atiyah1970] M. F. Atiyah, Global theory of elliptic operators, (1970), 21–30. MR0266247 (42 #1154) Zbl 0193.43601
- [Higson&Roe2000] N. Higson and J. Roe, Analytic
 -homology, Oxford University Press, Oxford, 2000. MR1817560 (2002c:58036) Zbl 1146.19004
-homology, Oxford University Press, Oxford, 2000. MR1817560 (2002c:58036) Zbl 1146.19004
- [Laures2003] G. Laures, An
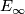 splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
- [Lawson&Michelsohn1989] H. B. Lawson and M. Michelsohn, Spin geometry, Princeton University Press, Princeton, NJ, 1989. MR1031992 (91g:53001) Zbl 0801.58017
- [Milnor1963a] J. Milnor, Spin structures on manifolds, Enseignement Math. (2) 9 (1963), 198–203. MR0157388 (28 #622) Zbl 0116.40403
- [Milnor1965] J. W. Milnor, Remarks concerning spin manifolds, in Differential and Combinatorial Topology, a Symposium in Honor of Marston Morse, (1965) 55–62. MR0180978 (31 #5208) Zbl 0132.19602
- [Rohlin1952] V. A. Rohlin, New results in the theory of four-dimensional manifolds, Doklady Akad. Nauk SSSR (N.S.) 84 (1952), 221–224. MR0052101 (14,573b)
- [Stong1966] R. E. Stong, Relations among characteristic numbers. II, Topology 5 (1966), 133–148. MR0192516 (33 #741) Zbl 0142.40902
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
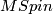 .
.
Preliminary results were by Novikov. The main calculation was achieved in [Anderson&Brown&Peterson1966] and [Anderson&Brown&Peterson1967].
[edit] 2 Invariants
The spin bordism class of a manifold is detected by  -cohomology (Stiefel-Whitney) and KO-theory (Pontryagin) characteristic numbers.
-cohomology (Stiefel-Whitney) and KO-theory (Pontryagin) characteristic numbers.
For a multi-index 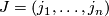 , we set
, we set 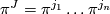 and
and 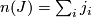 .
.
 -manifold
-manifold  induces a KO-orientation
induces a KO-orientation ![[M]\in KO_n(M)](/images/math/4/0/1/401c80af9787cadfd50c483e0a4e3289.png) , so that we can evaluate polynomials in the KO-Pontryagin classes
, so that we can evaluate polynomials in the KO-Pontryagin classes 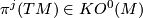 to get characteristic numbers
to get characteristic numbers ![\displaystyle \pi^J(M)=\langle \pi^J(TM), [M] \rangle \in KO_n(pt).](/images/math/e/f/1/ef11fdaca6fe169cbb99a2a7b7bc5cb1.png)
There is an interpretation of these characteristic numbers using index theory:
A feature of Spin manifolds  is that they possess Dirac operators,
is that they possess Dirac operators, 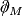 . The (Clifford-linear) Dirac operator can be considered as a representative of the fundamental class
. The (Clifford-linear) Dirac operator can be considered as a representative of the fundamental class ![[M]\in KO_n(M)](/images/math/4/0/1/401c80af9787cadfd50c483e0a4e3289.png) ,
see [Atiyah1970] and [Higson&Roe2000].
The characteristic numbers above can then be defined as the indices of the (Clifford-linear) Dirac operators obtained by twisting with the corresponding vector bundles.
The easiest case is the non-twisted one:
,
see [Atiyah1970] and [Higson&Roe2000].
The characteristic numbers above can then be defined as the indices of the (Clifford-linear) Dirac operators obtained by twisting with the corresponding vector bundles.
The easiest case is the non-twisted one: 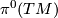 is the trivial bundle, and taking the index of the Dirac operator
is the trivial bundle, and taking the index of the Dirac operator 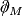 defines an element of
defines an element of 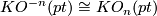 when
when  is n-dimensional. This gives rises to a ring homomorphism often called the
is n-dimensional. This gives rises to a ring homomorphism often called the  -invariant:
-invariant:
![\displaystyle \alpha : \Omega_*^{Spin} \longrightarrow KO_*, ~~~ [M] \longmapsto [\operatorname{ind} \partial\!\!\!/_M]=\alpha(M)=\pi^0(M).](/images/math/5/b/e/5befb82949e3197c345ca4ce92f695f5.png)
See [Lawson&Michelsohn1989].
For  divisible by 4, this invariant equals (up to a factor of 1/2 in dimensions congruent to 4 modulo 8) the
divisible by 4, this invariant equals (up to a factor of 1/2 in dimensions congruent to 4 modulo 8) the 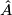 -genus of
-genus of  .
.
[edit] 3 Classification
[edit] 3.1 MSpin away from the prime 2 and at the prime 2
After inverting 2 the map of Thom spectra 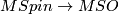 becomes a homotopy equivalence.
becomes a homotopy equivalence.
Using the Thom isomorphism 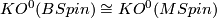 we get for each multi-index
we get for each multi-index 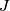 with
with 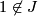 a map
a map 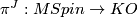 ,
which induces on homotopy groups the map
,
which induces on homotopy groups the map 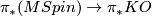 ,
, ![[M]\mapsto \pi^J(M)](/images/math/b/0/1/b01e5922e29db88139d86a642b5ef011.png) described above.
Anderson,Brown and Peterson show that
described above.
Anderson,Brown and Peterson show that 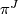 factorizes through
factorizes through 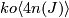 if
if  is even
and
is even
and 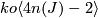 if
if  is odd. Hence the corresponding characteristic numbers vanish
for manifolds of smaller dimension.
is odd. Hence the corresponding characteristic numbers vanish
for manifolds of smaller dimension.
Similarly a Stiefel-Whitney class in 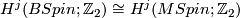 corresponds to a spectrum map
corresponds to a spectrum map 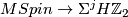 .
.
Theorem 3.1 [Anderson&Brown&Peterson1967].
There are classes 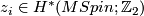 such that there is a 2-local homotopy equivalence
such that there is a 2-local homotopy equivalence
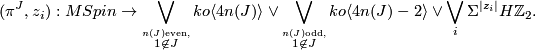
[Anderson&Brown&Peterson1966] also determine the Poincaré polynomial of 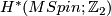 which allows to compute inductively
the degrees
which allows to compute inductively
the degrees 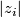 . The first
. The first 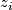 occurs in dimension
occurs in dimension 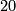 , and there are
, and there are 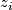 in all dimensions
in all dimensions 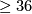 .
.
[edit] 3.2 Consequences
From this one can compute the additive structure of the spin bordism groups completely.
We get a contribution from each 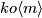 which is 0 below dimension
which is 0 below dimension  , and periodic of period 8 starting from dimension
, and periodic of period 8 starting from dimension  , with values
, with values
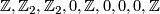 (here the first value corresponds to dimensions congruent to 0 modulo 8).
The contribution from
(here the first value corresponds to dimensions congruent to 0 modulo 8).
The contribution from 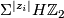 is a single
is a single  in dimension
in dimension 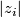 .
.
All  summands are in degrees divisible by 4, and there is no odd torsion in the spin cobordism groups.
All even torsion is of exponent 2, being of two types: that arising by products with a framed
summands are in degrees divisible by 4, and there is no odd torsion in the spin cobordism groups.
All even torsion is of exponent 2, being of two types: that arising by products with a framed  and that which maps monomorphically into unoriented cobordism.
and that which maps monomorphically into unoriented cobordism.
[edit] 3.3 Ring structure
Concerning the multiplicative structure, 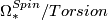 is the subring of an integral polynomial ring on classes
is the subring of an integral polynomial ring on classes 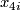 (dimension 4i)
consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8 [Stong1968].
Anderson, Brown and Peterson determine the structure of
(dimension 4i)
consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8 [Stong1968].
Anderson, Brown and Peterson determine the structure of 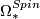 modulo
the ideal consisting of torsion mapping monomorphically into unoriented cobordism.
According to [Laures2003], the multiplicative structure of this ideal is still not completely known.
modulo
the ideal consisting of torsion mapping monomorphically into unoriented cobordism.
According to [Laures2003], the multiplicative structure of this ideal is still not completely known.
[edit] 4 Generators
[edit] 4.1 Low dimensions
The spin bordism groups up to dimension  are given in [Milnor1963a] without proof.
Milnor states that this is the result of a formibable calculation of
are given in [Milnor1963a] without proof.
Milnor states that this is the result of a formibable calculation of 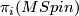 for
for 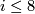 .
.
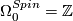 , generated by a point.
, generated by a point.
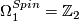 , generated by
, generated by 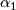 , the circle
with the "antiperiodic" spin structure.
, the circle
with the "antiperiodic" spin structure.
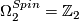 , generated by
, generated by 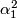 .
.
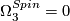 .
.
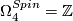 , generated by
, generated by 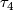 , the Kummer surface.
, the Kummer surface.
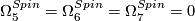 .
.
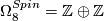 , generated by quaternionic projective space and a generator
, generated by quaternionic projective space and a generator 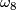 which equals 1/4 of the square of the Kummer surface.
which equals 1/4 of the square of the Kummer surface.
[edit] 4.2 Generators in all dimensions as given by the classification
By the theorem of Anderson, Brown and Peterson there exist manifolds
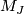 of dimension
of dimension 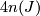 if
if  is even,
is even,
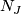 of dimension
of dimension 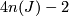 if
if  is odd, and
is odd, and 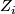 of dimension
of dimension 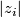 ,
such that the characteristic numbers
,
such that the characteristic numbers 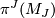 ,
, 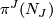 and
and 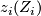 are odd.
For
are odd.
For  odd, let
odd, let 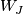 be a spin nullbordism of
be a spin nullbordism of 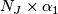 , and let
, and let
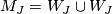 (using an orientation-reversing automorphism of
(using an orientation-reversing automorphism of  ). By [Stong1966] there exist manifolds
). By [Stong1966] there exist manifolds 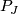 such that
such that
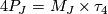 . If all
. If all 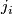 are even,
one can choose
are even,
one can choose 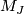 to be a product of quaternionic projective spaces.
to be a product of quaternionic projective spaces.
Then a basis for 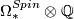 is given by
is given by
-
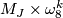 for
for 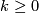
-
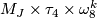 for
for 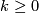 .
.
A basis for 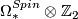 is given by
is given by
-
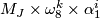 with
with 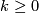 ,
, 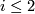 and
and  even,
even,
-
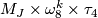 with
with 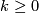 ,
,  even,
even,
-
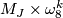 with
with 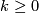 ,
,  odd,
odd,
-
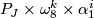 with
with 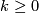 ,
, 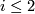 and
and  odd
odd
-
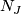 with
with  odd,
odd,
-
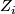 .
.
[edit] 5 Further topics
[edit] 5.1 Rohlin's theorem
Above we stated that the 4-dimensional spin bordism group 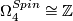 is generated
by the Kummer surface
is generated
by the Kummer surface 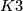 which has signature 16. Consequently we have the following important theorem of Rohlin (which of course was used in calculation of
which has signature 16. Consequently we have the following important theorem of Rohlin (which of course was used in calculation of 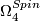 give above).
give above).
Theorem 5.1 [Rohlin1952].
The signature of every closed smooth spin  -manifold is divisible by
-manifold is divisible by 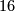 .
.
[edit] 5.2 Relationship with other bordism groups
- Framed bordism: the image of
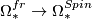 is 0 unless
is 0 unless 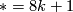 or
or 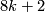 when it is
when it is  and detected by the
and detected by the  -invariant. Explicit generators are
-invariant. Explicit generators are 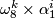 with
with 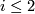 and
and 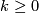 .
.
- Oriented bordism: the kernel of
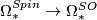 lies in dimensions
lies in dimensions 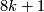 and
and 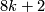 . It is a
. It is a  vector space with a basis
vector space with a basis 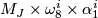 , for
, for  even, and
even, and 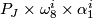 , for
, for  odd, where
odd, where 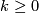 and
and 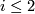 . It is also the ideal generated by the non-trivial class of
. It is also the ideal generated by the non-trivial class of 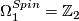 . The cokernel is a finite
. The cokernel is a finite  -torsion group which is trivial if and only if
-torsion group which is trivial if and only if 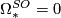 or equivalently
or equivalently 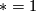 ,
,  ,
,  ,
,  , and
, and  . [Milnor1965] computed
. [Milnor1965] computed 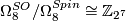 .
.
- Unoriented bordism: the image of
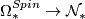 is all bordism classes for which the characteristic numbers divisible by
is all bordism classes for which the characteristic numbers divisible by 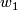 and
and 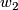 are zero. A basis for the image consists of the
are zero. A basis for the image consists of the 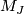 , for
, for  even, the
even, the 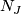 , for
, for  odd and the
odd and the 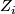 . The image is trivial for
. The image is trivial for  . In even dimensions it is additionally trivial for
. In even dimensions it is additionally trivial for 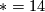 and
and 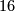 . In odd dimensions it is trivial for
. In odd dimensions it is trivial for 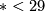 and also for
and also for 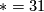 and
and 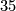 . Otherwise the image is non trivial.
. Otherwise the image is non trivial.
[edit] 6 References
- [Anderson&Brown&Peterson1966] D. W. Anderson, E. H. Brown and F. P. Peterson, Spin cobordism, Bull. Amer. Math. Soc. 72 (1966), 256–260. MR0190939 (32 #8349) Zbl 0156.21605
- [Anderson&Brown&Peterson1967] D. W. Anderson, E. H. Brown and F. P. Peterson, The structure of the Spin cobordism ring, Ann. of Math. (2) 86 (1967), 271–298. MR0219077 (36 #2160) Zbl 0156.21605
- [Atiyah1970] M. F. Atiyah, Global theory of elliptic operators, (1970), 21–30. MR0266247 (42 #1154) Zbl 0193.43601
- [Higson&Roe2000] N. Higson and J. Roe, Analytic
 -homology, Oxford University Press, Oxford, 2000. MR1817560 (2002c:58036) Zbl 1146.19004
-homology, Oxford University Press, Oxford, 2000. MR1817560 (2002c:58036) Zbl 1146.19004
- [Laures2003] G. Laures, An
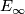 splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
splitting of spin bordism, Amer. J. Math. 125 (2003), no.5, 977–1027. MR2004426 (2004g:55007) Zbl 1058.55001
- [Lawson&Michelsohn1989] H. B. Lawson and M. Michelsohn, Spin geometry, Princeton University Press, Princeton, NJ, 1989. MR1031992 (91g:53001) Zbl 0801.58017
- [Milnor1963a] J. Milnor, Spin structures on manifolds, Enseignement Math. (2) 9 (1963), 198–203. MR0157388 (28 #622) Zbl 0116.40403
- [Milnor1965] J. W. Milnor, Remarks concerning spin manifolds, in Differential and Combinatorial Topology, a Symposium in Honor of Marston Morse, (1965) 55–62. MR0180978 (31 #5208) Zbl 0132.19602
- [Rohlin1952] V. A. Rohlin, New results in the theory of four-dimensional manifolds, Doklady Akad. Nauk SSSR (N.S.) 84 (1952), 221–224. MR0052101 (14,573b)
- [Stong1966] R. E. Stong, Relations among characteristic numbers. II, Topology 5 (1966), 133–148. MR0192516 (33 #741) Zbl 0142.40902
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010