Spin bordism
| Line 8: | Line 8: | ||
<wikitex>; | <wikitex>; | ||
| + | {{cite|Stong1968}} | ||
Preliminary results were by Novikov. The main | Preliminary results were by Novikov. The main | ||
calculation is due to Anderson, Brown, and Peterson | calculation is due to Anderson, Brown, and Peterson | ||
Revision as of 22:44, 26 January 2010
Contents |
1 Introduction
The spin bordism groups 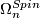 of manifolds with spin structures are the homotopy groups of the Thom spectrum
of manifolds with spin structures are the homotopy groups of the Thom spectrum 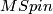 .
.
2 Calculation
[Stong1968]
Preliminary results were by Novikov. The main
calculation is due to Anderson, Brown, and Peterson
[Anderson&Brown&Peterson1966]
who showed that all torsion is of order 2, being of two types: that arising by products with a framed  and that which maps monomorphically into unoriented cobordism.
and that which maps monomorphically into unoriented cobordism. 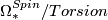 is the subring of an integral polynomial ring on classes
is the subring of an integral polynomial ring on classes 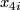 (dimension 4i) consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8.
(dimension 4i) consisting of all classes of dimension a multiple of 8 and twice the classes whose dimension is not a multiple of 8.
Characteristic numbers: Cobordism is determined by  cohomology and
cohomology and 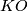 -theory characteristic numbers.
-theory characteristic numbers.
Relation to framed bordism: The image of framed cobordism is 0 except in dimensions 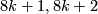 where it is
where it is  .
.
Relation to oriented bordism:
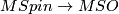 is an equivalence after inverting 2.
The kernel of the map from spin to oriented bordism is in dimensions
is an equivalence after inverting 2.
The kernel of the map from spin to oriented bordism is in dimensions 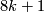 and
and 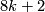 only and is the part generated by framed manifolds. It is the ideal generated by the non-trivial class of degree 1.
only and is the part generated by framed manifolds. It is the ideal generated by the non-trivial class of degree 1.
The image in unoriented cobordism is all classes for which the characteristic numbers divisible by 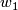 and
and 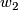 are zero.
are zero.
3 KO-Characteristic classes
%This should probably get its own page.%
The KO-Pontryagin classes 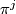 are defined by setting
are defined by setting
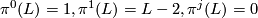 for
for 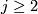 for complex line bundles L and then requiring naturality and
for complex line bundles L and then requiring naturality and
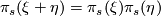 where
where 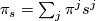 .
Here
.
Here  and
and 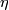 are oriented bundles.
In fact, these properties determine
are oriented bundles.
In fact, these properties determine 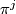 because the group
because the group 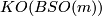 injects into
injects into ![K(BT^{[m/2]})](/images/math/3/6/4/364dfbae4b2336e2bafa5ef956102a4f.png) under the
complexification of the map which is induced by the restriction to the maximal torus
under the
complexification of the map which is induced by the restriction to the maximal torus ![T^{[m/2]}](/images/math/f/6/2/f62a2f55a50b2ecc510a731975035028.png) (compare [Anderson&Brown&Peterson1966]).
For
(compare [Anderson&Brown&Peterson1966]).
For 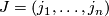 we set
we set 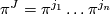 .
Such a class gives a map
.
Such a class gives a map 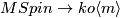 .
.
Theorem [Anderson&Brown&Peterson1966] 3.1. There is a 2-local homotopy equivalence
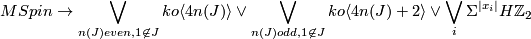
4 Low dimensions
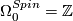 , generated by a point.
, generated by a point.
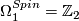 , generated by the circle
with the "antiperiodic" spin structure.
, generated by the circle
with the "antiperiodic" spin structure.
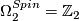 , generated by the square of the generator of the first bordism group.
, generated by the square of the generator of the first bordism group.
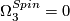 .
.
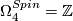 , generated by the Kummer surface.
, generated by the Kummer surface.
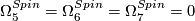 .
.
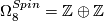 , generated by quaternionic projective space, and 1/4 of the square of the Kummer surface.
, generated by quaternionic projective space, and 1/4 of the square of the Kummer surface.
5 References
- [Anderson&Brown&Peterson1966] D. W. Anderson, E. H. Brown and F. P. Peterson, Spin cobordism, Bull. Amer. Math. Soc. 72 (1966), 256–260. MR0190939 (32 #8349) Zbl 0156.21605
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
|
This page has not been refereed. The information given here might be incomplete or provisional. |