Some calculations involving configuration spaces of distinct points
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem.
For a subset 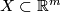 ,
, 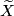 denotes the deleted product of
denotes the deleted product of  , i.e.
, i.e. 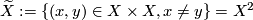 minus the diagonal. This is the configuration space of ordered pairs of distinct points of K.
minus the diagonal. This is the configuration space of ordered pairs of distinct points of K.
Definition 1.1.[of the Haefliger-Wu invariant  ]
]
The Haefliger-Wu invariant
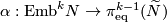 is induced by the Gauss map, also denoted by
is induced by the Gauss map, also denoted by  .
The Gauss map assigns to an individual embedding
.
The Gauss map assigns to an individual embedding 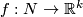 an equivariant map
an equivariant map 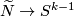 defined by the formula
defined by the formula
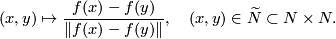
Theorem 1.2.
The Haefliger-Wu invariant 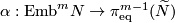 is one-to-one for
is one-to-one for 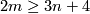 .
.
2 Construction and examples
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...