Some calculations involving configuration spaces of distinct points
From Manifold Atlas
Revision as of 13:55, 2 April 2020 by Mikhail Fedorov (Talk | contribs)
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
...
2 Construction and examples
For a manifold  ,
, 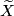 denotes the deleted product of
denotes the deleted product of  , i.e.
, i.e. 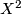 minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
Definition 2.1.[of the Haefliger-Wu invariant  ]
]
The Haefliger-Wu invariant
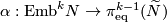 is induced by the Gauss map, also denoted by
is induced by the Gauss map, also denoted by  .
The Gauss map assigns to an individual embedding
.
The Gauss map assigns to an individual embedding 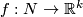 an equivariant map
an equivariant map 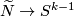 defined by the formula
defined by the formula
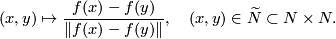
The Haefliger-Wu invariant and the Gauss map are analogously defined for  ; we will denote them by
; we will denote them by 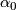 in this case.
in this case.
{{{1}}} 2.2.
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...