Some calculations involving configuration spaces of distinct points
m (→Introduction) |
(→Uniqueness theorems) |
||
| Line 43: | Line 43: | ||
== Uniqueness theorems == | == Uniqueness theorems == | ||
<wikitex>; | <wikitex>; | ||
| − | {{beginthm| | + | {{beginthm|Lemma}}\label{th::unknotting} |
Assume that $N$ is a compact $n$-manifold and either | Assume that $N$ is a compact $n$-manifold and either | ||
| Line 50: | Line 50: | ||
(b) $N$ is connected and $m \ge 2n+1 \ge 5$. | (b) $N$ is connected and $m \ge 2n+1 \ge 5$. | ||
| − | Then | + | Then every two every two equivariant maps $f, g:\widetilde N\to S^{m-1}$ are equivariantly homotopic. |
{{endthm}} | {{endthm}} | ||
| − | In cases (a- | + | ''Proof.'' |
| − | + | In cases (a-b) inequality $2m\ge3n+4$ is clearly satisfied. | |
| − | + | ||
Take an arbitrary equivariant triangulation $T$ of $\widetilde N$. | Take an arbitrary equivariant triangulation $T$ of $\widetilde N$. | ||
| Line 65: | Line 64: | ||
(b) Since $\widetilde{N}$ has non-empty boundary, there exists an equivariant deformational retraction of $\widetilde{N}$ to an equivariant $(2n-1)$-subcomplex of $T$. A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on $\widetilde{N}$. | (b) Since $\widetilde{N}$ has non-empty boundary, there exists an equivariant deformational retraction of $\widetilde{N}$ to an equivariant $(2n-1)$-subcomplex of $T$. A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on $\widetilde{N}$. | ||
| + | QED | ||
</wikitex> | </wikitex> | ||
Revision as of 15:36, 5 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
‘The complement of the diagonal’ and ‘the Gauss map’ ideas play a great role in different branches of mathematics. The Haefliger-Wu invariant is a manifestation of these ideas in the theory of embeddings. The complement to the diagonal idea originated from two celebrated theorems: the Lefschetz Fixed Point Theorem and the Borsuk-Ulam Antipodes Theorem.
The deleted product 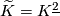 is
is
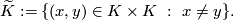 This is the configuration space of ordered pairs of distinct points of
This is the configuration space of ordered pairs of distinct points of  .
.
Suppose that 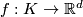 is an embedding of a subset
is an embedding of a subset 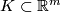 .
Then the map
.
Then the map 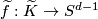 is well-defined by the Gauss formula
is well-defined by the Gauss formula
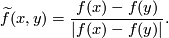
We have 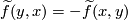 , i.e. this map is equivariant with respect to the `exchanging factors' involution
, i.e. this map is equivariant with respect to the `exchanging factors' involution
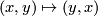 on
on 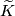 and the antipodal involution on
and the antipodal involution on 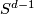 .
Thus the existence of an equivariant map
.
Thus the existence of an equivariant map 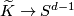 is a necessary condition for the embeddability of
is a necessary condition for the embeddability of  in
in 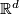 .
.
Definition 1.1.[of the Haefliger-Wu invariant  ]
]
The Haefliger-Wu invariant
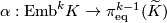 is induced by the Gauss map, also denoted by
is induced by the Gauss map, also denoted by  .
.
Theorem 1.2.
The Haefliger-Wu invariant 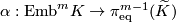 is one-to-one for
is one-to-one for  .
.
2 Uniqueness theorems
Lemma 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 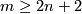 or
or
(b)  is connected and
is connected and 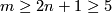 .
.
Then every two every two equivariant maps 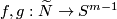 are equivariantly homotopic.
are equivariantly homotopic.
Proof.
In cases (a-b) inequality 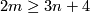 is clearly satisfied.
is clearly satisfied.
Take an arbitrary equivariant triangulation  of
of 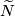 .
.
(a) One can easily construct an equivariant homotopy between restrictions of  and
and  on vertices of
on vertices of  .
By general position a homotopy of
.
By general position a homotopy of 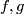 on the boundary of a
on the boundary of a  -simplex can be extended to a homotopy on the whole
-simplex can be extended to a homotopy on the whole  -simplex since
-simplex since 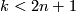 .
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
.
We extend equivariant homotopy on symmetric simplices in the symmetric way, so we obtain an equivariant homotopy.
(b) Since 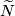 has non-empty boundary, there exists an equivariant deformational retraction of
has non-empty boundary, there exists an equivariant deformational retraction of 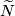 to an equivariant
to an equivariant 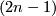 -subcomplex of
-subcomplex of  . A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on
. A homotopy on the subcomplex can by constructed similarly to case~(a). This homotopy can be extended to a homotopy on 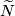 .
QED
.
QED
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...