Some calculations involving configuration spaces of distinct points
(Difference between revisions)
(Created page with " <!-- COMMENT: To achieve a unified layout, along with using the template below, please OBSERVE the following: besides, $...$ and $$...$$, you should use two environments: ...") |
m (→Construction and examples) |
||
| Line 20: | Line 20: | ||
== Construction and examples == | == Construction and examples == | ||
<wikitex>; | <wikitex>; | ||
| − | ... | + | For a manifold $X$, $\widetilde X$ denotes ''the deleted product'' of $X$, i.e. $X^2$ minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution. |
| + | {{theorem|Definition}}[of the Haefliger-Wu invariant $\alpha$] | ||
| + | \label{DefHaef} | ||
| + | The Haefliger-Wu invariant | ||
| + | $\alpha:\mathrm{Emb}^{k}N\to \pi_{\mathrm{eq}}^{k-1}(\widetilde{N})$ | ||
| + | is induced by the Gauss map, also denoted by $\alpha$. | ||
| + | The Gauss map assigns to an individual embedding $f:N\to\R^{k}$ | ||
| + | an equivariant map $\widetilde{N}\to S^{k-1}$ | ||
| + | defined by the formula | ||
| + | $$ | ||
| + | (x,y)\mapsto | ||
| + | \frac{f(x)-f(y)} | ||
| + | {\|f(x)-f(y)\|}, | ||
| + | \quad | ||
| + | (x,y)\in\widetilde{N}\subset N\times N. | ||
| + | $$ | ||
| + | The Haefliger-Wu invariant and the Gauss map are analogously defined for $N_0$; we will denote them by $\alpha_0$ in this case. | ||
| + | {{definition}} | ||
</wikitex> | </wikitex> | ||
Revision as of 13:54, 2 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
...
2 Construction and examples
For a manifold  ,
, 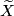 denotes the deleted product of
denotes the deleted product of  , i.e.
, i.e. 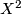 minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
Template:Theorem[of the Haefliger-Wu invariant
minus an open tubular neighborhood of the diagonal. It is a manifold with boundary and has the standard free involution.
Template:Theorem[of the Haefliger-Wu invariant  ]
The Haefliger-Wu invariant
]
The Haefliger-Wu invariant
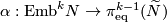 is induced by the Gauss map, also denoted by
is induced by the Gauss map, also denoted by  .
The Gauss map assigns to an individual embedding
.
The Gauss map assigns to an individual embedding 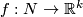 an equivariant map
an equivariant map 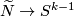 defined by the formula
defined by the formula
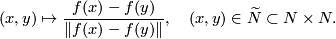
The Haefliger-Wu invariant and the Gauss map are analogously defined for  ; we will denote them by
; we will denote them by 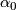 in this case.
Template:Definition
in this case.
Template:Definition
3 Invariants
...
4 Classification/Characterization
...
5 Further discussion
...