Smoothing the Kervaire manifold (Ex)
From Manifold Atlas
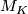 be the
be the 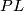 Kervaire
Kervaire 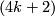 -manifold and let
-manifold and let 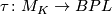 and let
and let 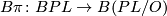 be the canonical map. In addition let
be the canonical map. In addition let 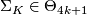 be the Kervaire sphere and let
be the Kervaire sphere and let 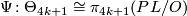
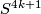 .
.
Exercise 0.1.
- Show that the Spivak normal fibration of
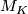 admits a vector bundle reduction.
admits a vector bundle reduction.
- Determine the homotopy class of
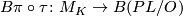 in terms of
in terms of 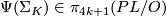 .
.