Sandbox
|
The sandbox is the page where you can experiment with the wiki syntax. Feel free to write nonsense or clear the page whenever you want. |
Contents |
1 Images
Theorem 1.1. We have
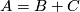 (1.1)
(1.1)By Theorem
 (1.2)
(1.2)Theorem 1.2. Frog
Here is some text leading up to an equation
1.3.
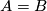
Here is some more text after the equation to see how it looks.
Here is some text leading up to an equation
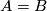
Here is some more text after the equation to see how it looks.
4k 8 12 16 20 24 28 32 order bP4k 22.7 25.31 26.127 29.511 210.2047.691 213.8191 214.16384.3617
k 1 2 3 4 5 6 7 8 Bk 1/6 1/30 1/42 1/30 5/66 691/2730 7/6 3617/510
Dim n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 order Θn 1 1 1 1 1 1 28 2 8 6 992 1 3 2 16256 2 16 16 523264 24 bPn+1 1 1 1 1 1 1 28 1 2 1 992 1 1 1 8128 1 2 1 261632 1 Θn/bPn+1 1 1 1 1 1 1 1 2 2×2 6 1 1 3 2 2 2 2×2×2 8×2 2 24 πnS/J 1 2 1 1 1 2 1 2 2×2 6 1 1 3 2×2 2 2 2×2×2 8×2 2 24 index - 2 - - - 2 - - - - - - - 2 - - - - - -
Extension DPL (warning): current configuration allows execution of DPL code from protected pages only.
Just a fest 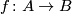 .
.
a theorem 1.4.
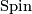
by theorem 1.4
- Amsterdam
- Rotterdam
- The Hague
[Mess1990]
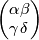
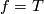
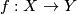
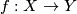
bold italic emphasis
2 Tests
[Ranicki1981] [Milnor1956] [Milnor1956, Theorem 1] [Milnor1956] [Milnor1956, Theorem 1] Frog
Proof.

3 Section
3.1 Subsection
Refert to subsection 3.1
Theorem 3.1. test
Refer to theorem 3.1
4 Section
An inter-Wiki link.
Another [1]; inter-Wiki link.
dfa[2]