Sandbox

From Manifold Atlas

(Difference between revisions)

Jump to: navigation, search

Latest revision as of 07:31, 15 October 2019

The sandbox is the page where you can experiment with the wiki syntax. Feel free to write nonsense or clear the page whenever you want.

[edit] 1 File Creation Practice

Click here to access the pdf file.

[edit] 2 Testing equation numbering

(1) $A = B$ $  <stepsectioncounter/> [[Media:4manifolds.pdf|link text]] * [[Media:New_submission.pdf|Click here to access the pdf file]]. == Testing equation numbering == <wikitex>; \begin{equation} \label{eq:1} A = B \end{equation} Here is a reference to equation \ref{eq:1} </wikitex> == Still testing equation numbering == <wikitex>; \begin{equation}\label{test} C = D \end{equation} \ref{test} </wikitex> == Lists== <wikitex>; <ol style="list-tsyle-type:lower-roman> <li>Frog</li> </ol> $$ A \xrightarrow{f} B$$ $--$ </wikitex> {{beginthm|Theorem|\cite{Penrose&Whitehead&Zeeman1961}}}\label{thm:2.1} For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$. {{endthm}} {{beginrem|Remark}} For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. {{endrem}} {{beginthm|Theorem|\cite{Whitney1944}}}\label{thm:2.2} For every closed m--dimensional $C^{\infty}$--manifold $M$ there exists a $C^{\infty}$--embedding $M \hookrightarrow \R^{2m}$. {{endthm}} {{beginrem|Remark}} For a more modern exposition see also \cite{Adachi1993|p. 67ff}. {{endrem}} \begin{theorem} \label{thm:1} We have $f \colon X \to Y$ \end{theorem} Reference \ref{thm:1} By Theorem {{equation|$\alpha$|1.2}} {{eqref|1.2}} {{begineq|eqtest|$\alpha$}}<label>qtest</label>{{endeq}} {{beginthm|Theorem}} Frog {{endthm}} \ref{qtest} \ref{eqtest} Here is some text leading up to an equation {{beginrem| }} $$ A = B $$ {{endrem}} Here is some more text after the equation to see how it looks. Here is some text leading up to an equation $$ A = B $$ Here is some more text after the equation to see how it looks. :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! 4k !! 8 !! 12 !! 16 !! 20 !! 24 !! 28 !! 32 |- ! order bP4k | 22.7 || 25.31 || 26.127|| 29.511|| 210.2047.691 || 213.8191 || 214.16384.3617 |- |}  :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! k !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 |- ! Bk | 1/6 || 1/30 || 1/42 || 1/30 || 5/66 || 691/2730 || 7/6 || 3617/510 || |- |} :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! Dim n !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 !! 9 !! 10 !! 11 !! 12 !! 13 !! 14 !! 15 !! 16 !! 17 !! 18 !! 19 !! 20 |- ! order Θ''n'' | 1 || 1 || 1 || 1 || 1 || 1 || 28 || 2 || 8 || 6 || 992 || 1 || 3 || 2 || 16256 || 2 || 16 || 16 || 523264 || 24 |- !''bP''''n''+1 | 1 || 1 || 1 || 1 || 1 || 1 || 28 || 1 || 2 || 1 || 992 || 1 || 1 || 1 || 8128 || 1 || 2 || 1 || 261632 || 1 |- !Θ''n''/''bP''''n''+1 | 1 || 1 || 1 || 1 || 1 || 1 || 1 || 2 ||2×2 || 6 || 1 || 1 || 3 || 2 || 2 || 2 || 2×2×2 || 8×2 || 2 || 24 |- !π''n''''S''/''J'' | 1 || 2 || 1 || 1 || 1 || 2 || 1 || 2 || 2×2 || 6 || 1 || 1 || 3 || 2×2 || 2 || 2 || 2×2×2 || 8×2 || 2 || 24 |- !index | - || 2 || - || - || - || 2 || - || - || - || - || - || - || - || 2 || - || - || - || - || - || - |} [[Media:Spaceform.tiff|link text]] $$ f \colon X \to Y $$ <DPL> namespace=Main nottitlematch=Main_Page|Sandbox|Links ordermethod=lastedit order=descending minoredits=exclude author=%Diarmuid Crowley% count=10 </DPL> Just a fest $f \colon A \to B$. $\Q$ {{beginthm|a theorem}} \label{thma} {{endthm}} $\text{Spin}$ by theorem \ref{thma} <ol start="9"> <li>Amsterdam</li> <li>Rotterdam</li> <li>The Hague</li> </ol> <nowiki>[</nowiki>[[#{{anchorencode:Mess1990}}|Mess1990]]<nowiki>]</nowiki>{{#RefAdd:Mess1990}}  $\left( \begin{array}{ll} \alpha & \beta \ \gamma & \delta \end{array} \right)$ $f = T$ $ f : X \to Y$ $$ f : X \to Y $$ $\Ker$ $\mathscr{A}$ $\mathscr{B}$ \bf{ bold} \it{italic} \em{emphasis} </wikitex> [[Image:Foliation.png|thumb|300px|3-dimensional Reeb foliation]] == Tests == {{citeD|Ranicki1981}} {{cite|Milnor1956}} {{cite|Milnor1956|Theorem 1}} {{citeD|Milnor1956}} {{citeD|Milnor1956|Theorem 1}} {{citeD2|Milnor1956|Frog}} <wikitex>; {{beginproof}} {{endproof}} </wikitex> == Section == === Subsection === \label{subsection} Refert to subsection \ref{subsection} \begin{theorem} \label{thm} test \end{theorem} Refer to theorem \ref{thm} == Section == <wikitex>; '''$\textup{CW}_0$''' An [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. Another <ref> Test1 </ref> [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. dfa<ref>Test2</ref> </wikitex> ==Footnotes== <references/> ==References== {{#RefList:}}  <stepsectioncounter/> [[Media:4manifolds.pdf|link text]] * [[Media:New_submission.pdf|Click here to access the pdf file]]. == Testing equation numbering == <wikitex>; \begin{equation} \label{eq:1} A = B \end{equation} Here is a reference to equation \ref{eq:1} </wikitex> == Still testing equation numbering == <wikitex>; \begin{equation}\label{test} C = D \end{equation} \ref{test} </wikitex> == Lists== <wikitex>; <ol style="list-tsyle-type:lower-roman> <li>Frog</li> </ol> $$ A \xrightarrow{f} B$$ $--$ </wikitex> {{beginthm|Theorem|\cite{Penrose&Whitehead&Zeeman1961}}}\label{thm:2.1} For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$. {{endthm}} {{beginrem|Remark}} For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. {{endrem}} {{beginthm|Theorem|\cite{Whitney1944}}}\label{thm:2.2} For every closed m--dimensional $C^{\infty}$--manifold $M$ there exists a $C^{\infty}$--embedding $M \hookrightarrow \R^{2m}$. {{endthm}} {{beginrem|Remark}} For a more modern exposition see also \cite{Adachi1993|p. 67ff}. {{endrem}} \begin{theorem} \label{thm:1} We have $f \colon X \to Y$ \end{theorem} Reference \ref{thm:1} By Theorem {{equation|$\alpha$|1.2}} {{eqref|1.2}} {{begineq|eqtest|$\alpha$}}<label>qtest</label>{{endeq}} {{beginthm|Theorem}} Frog {{endthm}} \ref{qtest} \ref{eqtest} Here is some text leading up to an equation {{beginrem| }} $$ A = B $$ {{endrem}} Here is some more text after the equation to see how it looks. Here is some text leading up to an equation $$ A = B $$ Here is some more text after the equation to see how it looks. :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! 4k !! 8 !! 12 !! 16 !! 20 !! 24 !! 28 !! 32 |- ! order bP4k | 22.7 || 25.31 || 26.127|| 29.511|| 210.2047.691 || 213.8191 || 214.16384.3617 |- |}  :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! k !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 |- ! Bk | 1/6 || 1/30 || 1/42 || 1/30 || 5/66 || 691/2730 || 7/6 || 3617/510 || |- |} :{| border="1" cellpadding="2" class="wikitable" style="text-align:center" |- ! Dim n !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 !! 9 !! 10 !! 11 !! 12 !! 13 !! 14 !! 15 !! 16 !! 17 !! 18 !! 19 !! 20 |- ! order Θ''n'' | 1 || 1 || 1 || 1 || 1 || 1 || 28 || 2 || 8 || 6 || 992 || 1 || 3 || 2 || 16256 || 2 || 16 || 16 || 523264 || 24 |- !''bP''''n''+1 | 1 || 1 || 1 || 1 || 1 || 1 || 28 || 1 || 2 || 1 || 992 || 1 || 1 || 1 || 8128 || 1 || 2 || 1 || 261632 || 1 |- !Θ''n''/''bP''''n''+1 | 1 || 1 || 1 || 1 || 1 || 1 || 1 || 2 ||2×2 || 6 || 1 || 1 || 3 || 2 || 2 || 2 || 2×2×2 || 8×2 || 2 || 24 |- !π''n''''S''/''J'' | 1 || 2 || 1 || 1 || 1 || 2 || 1 || 2 || 2×2 || 6 || 1 || 1 || 3 || 2×2 || 2 || 2 || 2×2×2 || 8×2 || 2 || 24 |- !index | - || 2 || - || - || - || 2 || - || - || - || - || - || - || - || 2 || - || - || - || - || - || - |} [[Media:Spaceform.tiff|link text]] $$ f \colon X \to Y $$ <DPL> namespace=Main nottitlematch=Main_Page|Sandbox|Links ordermethod=lastedit order=descending minoredits=exclude author=%Diarmuid Crowley% count=10 </DPL> Just a fest $f \colon A \to B$. $\Q$ {{beginthm|a theorem}} \label{thma} {{endthm}} $\text{Spin}$ by theorem \ref{thma} <ol start="9"> <li>Amsterdam</li> <li>Rotterdam</li> <li>The Hague</li> </ol> <nowiki>[</nowiki>[[#{{anchorencode:Mess1990}}|Mess1990]]<nowiki>]</nowiki>{{#RefAdd:Mess1990}}  $\left( \begin{array}{ll} \alpha & \beta \ \gamma & \delta \end{array} \right)$ $f = T$ $ f : X \to Y$ $$ f : X \to Y $$ $\Ker$ $\mathscr{A}$ $\mathscr{B}$ \bf{ bold} \it{italic} \em{emphasis} </wikitex> [[Image:Foliation.png|thumb|300px|3-dimensional Reeb foliation]] == Tests == {{citeD|Ranicki1981}} {{cite|Milnor1956}} {{cite|Milnor1956|Theorem 1}} {{citeD|Milnor1956}} {{citeD|Milnor1956|Theorem 1}} {{citeD2|Milnor1956|Frog}} <wikitex>; {{beginproof}} {{endproof}} </wikitex> == Section == === Subsection === \label{subsection} Refert to subsection \ref{subsection} \begin{theorem} \label{thm} test \end{theorem} Refer to theorem \ref{thm} == Section == <wikitex>; '''$\textup{CW}_0$''' An [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. Another <ref> Test1 </ref> [[map-eds:Manifold Atlas:Projects in the Atlas|inter-Wiki link]]. dfa<ref>Test2</ref> </wikitex> ==Footnotes== <references/> ==References== {{#RefList:}}A = B$

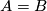
Here is a reference to equation 1

[edit] 3 Still testing equation numbering

(2) $C = D$ $C = D$

2

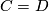
[edit] 4 Lists

Frog

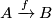
$\displaystyle A \xrightarrow{f} B$ $\displaystyle A \xrightarrow{f} B$

$--$

Theorem 5.1 [Penrose&Whitehead&Zeeman1961]. For every compact $m$--dimensional PL-manifold $M$ there exists a PL--embedding $ M \hookrightarrow \R^{2m}$.

Remark 5.2. For a good exposition of Theorem 5.1 see also [Rourke&Sanderson1972a, p. 63].

Theorem 5.3 [Whitney1944]. For every closed m--dimensional $C^{\infty}$--manifold $M$ there exists a $C^{\infty}$--embedding $M \hookrightarrow \R^{2m}$.

Remark 5.4. For a more modern exposition see also [Adachi1993, p. 67ff].

Theorem 5.5. We have $f \colon X \to Y$

Reference 5.5

By Theorem

$\alpha$(1.2)

1.2

(3)$\alpha$eqtest

Theorem 5.6. Frog

3 \ref{eqtest}

Here is some text leading up to an equation

5.7. $$ A = B $$

Here is some more text after the equation to see how it looks.

Here is some text leading up to an equation $$ A = B $$ Here is some more text after the equation to see how it looks.

4k	8	12	16	20	24	28	32
order bP_4k	2².7	2⁵.31	2⁶.127	2⁹.511	2¹⁰.2047.691	2¹³.8191	2¹⁴.16384.3617

k	1	2	3	4	5	6	7	8
B_k	1/6	1/30	1/42	1/30	5/66	691/2730	7/6	3617/510

Dim n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
order Θ_n	1	1	1	1	1	1	28	2	8	6	992	1	3	2	16256	2	16	16	523264	24
bP_n+1	1	1	1	1	1	1	28	1	2	1	992	1	1	1	8128	1	2	1	261632	1
Θ_n/bP_n+1	1	1	1	1	1	1	1	2	2×2	6	1	1	3	2	2	2	2×2×2	8×2	2	24
π_n^S/J	1	2	1	1	1	2	1	2	2×2	6	1	1	3	2×2	2	2	2×2×2	8×2	2	24
index	-	2	-	-	-	2	-	-	-	-	-	-	-	2	-	-	-	-	-	-

link text

$$ f \colon X \to Y $$

Extension DPL (warning): current configuration allows execution of DPL code from protected pages only.

Just a fest $f \colon A \to B$.

$\Q$

a theorem 5.8.

$\text{Spin}$

by theorem 5.8

Amsterdam
Rotterdam
The Hague

[Mess1990]

$\left( \begin{array}{ll} \alpha & \beta \\ \gamma & \delta \end{array} \right)$

$f = T$

$ f : X \to Y$

$$ f : X \to Y $$

$\Ker$

$\mathscr{A}$ $\mathscr{B}$

bold italic emphasis

</wikitex>

File:Foliation.png

3-dimensional Reeb foliation

[edit] 5 Tests

[Ranicki1981] [Milnor1956] [Milnor1956, Theorem 1] [Milnor1956] [Milnor1956, Theorem 1] Frog

Proof.

$\square$ $\square$

[edit] 6 Section

[edit] 6.1 Subsection

Refert to subsection 7.1

Theorem 7.1. test

Refer to theorem 7.1

[edit] 7 Section

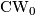
$\textup{CW}_0$

An inter-Wiki link.

Another ^[1]; inter-Wiki link.

dfa^[2]

[edit] 8 Footnotes

↑ Test1
↑ Test2

[edit] 9 References

[Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
[Mess1990] G. Mess, Examples of Poincaré duality groups, Proc. Amer. Math. Soc. 110 (1990), no.4, 1145–1146. MR1019274 (91c:20075) Zbl 0709.57025
[Milnor1956] J. Milnor, On manifolds homeomorphic to the 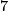$7$ -sphere, Ann. of Math. (2) 64 (1956), 399–405. MR0082103 (18,498d) Zbl 0072.18402
[Penrose&Whitehead&Zeeman1961] R. Penrose, J. Whitehead and E. Zeeman, Imbedding of manifolds in Euclidean space., Ann. of Math. 73 (1961) 613–623. MR0124909 (23 #A2218) Zbl 0113.38101
[Rourke&Sanderson1972a] C. P. Rourke and B. J. Sanderson, Introduction to piecewise-linear topology, Springer-Verlag, 1972. MR0350744 (50 #3236) Zbl 0477.57003
[Whitney1944] H. Whitney, The self-intersections of a smooth 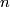$n$ -manifold in 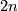$2n$ -space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237

[0] Test1

[1] Test2

[1]

[2]

Sandbox

Latest revision as of 07:31, 15 October 2019

Contents

[edit] 1 File Creation Practice

[edit] 2 Testing equation numbering

[edit] 3 Still testing equation numbering

[edit] 4 Lists

[edit] 5 Tests

[edit] 6 Section

[edit] 6.1 Subsection

[edit] 7 Section

[edit] 8 Footnotes

[edit] 9 References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Interaction

Toolbox

@@ Line 14: / Line 14: @@
 <stepsectioncounter/>
-[[Media:4manifolds.pdf|link text]]
+== File Creation Practice ==
-* [[Media:New_submission.pdf|Click here to access the pdf file]].
+[[Media:New_submission.pdf|Click here to access the pdf file]].
 == Testing equation numbering ==