Sandbox
m |
m |
||
| Line 37: | Line 37: | ||
{{endthm}} | {{endthm}} | ||
| − | {{beginthm|Theorem}} | + | {{beginthm|Theorem|}} |
For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. | For a good exposition of Theorem \ref{thm:2.1} see also \cite{Rourke&Sanderson1972a|p. 63}. | ||
{{endthm}} | {{endthm}} | ||
| Line 45: | Line 45: | ||
{{endthm}} | {{endthm}} | ||
| − | {{beginrem|Remark}} | + | {{beginrem|Remark|}} |
For a more modern exposition see also \cite{Adachi1993|p. 67ff}. | For a more modern exposition see also \cite{Adachi1993|p. 67ff}. | ||
{{endrem}} | {{endrem}} | ||
Revision as of 17:30, 24 April 2013
|
The sandbox is the page where you can experiment with the wiki syntax. Feel free to write nonsense or clear the page whenever you want. |
Contents |
1 Images
|
The user responsible for this page is Ulrich Koschorke. No other user may edit this page at present. |
|
This page is being independently reviewed under the supervision of the Editorial Board. |
Definition
We work in a fixed category CAT of topological, piecewise linear, 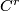 -differentiable
-differentiable 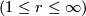 or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them.
or real analytic manifolds (second countable, Hausdorff, without boundary) and maps between them.
Let 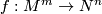 be such a map between manifolds of the indicated dimensions
be such a map between manifolds of the indicated dimensions 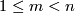 .
.
Definition 3.1.
We call  an embedding (and we write
an embedding (and we write 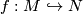 ) if
) if  is an immersion which maps
is an immersion which maps  homeomorphically onto its image.
homeomorphically onto its image.
It follows that an embedding cannot have selfintersections. But even an injective immersion need not be an embedding; e. g. the figure six 6
is the image of a smooth immersion but not of an embedding. Note that in the topological and piecewise linear categories,CAT = TOP or PL, our definition yields locally flat embeddings. In these categories there are other concepts of embeddings - e.g. wild embeddings - which are not locally flat: the condition
of local flatness is implied by our definition of immersion. Embeddings (and immersions) into familiar target manifolds such as 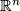 may help to visualize abstractly defined manifolds. E. g. all smooth surfaces can be immersed into
may help to visualize abstractly defined manifolds. E. g. all smooth surfaces can be immersed into 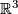 ; but nonorientable surfaces (such as the projective plane and the Klein bottle) allow no embeddings into
; but nonorientable surfaces (such as the projective plane and the Klein bottle) allow no embeddings into 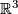 .
.
2 Existence of embeddings
Theorem 4.1 [Penrose&Whitehead&Zeeman1961].
For every compact  --dimensional PL-manifold
--dimensional PL-manifold  there exists a PL--embedding
there exists a PL--embedding 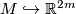 .
.
Theorem 4.2. For a good exposition of Theorem 4.1 see also [Rourke&Sanderson1972a, p. 63].
Theorem 4.3 [Whitney1944].
For every closed m--dimensional 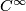 --manifold
--manifold  there exists a
there exists a 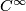 --embedding
--embedding 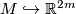 .
.
Remark 4.4. For a more modern exposition see also [Adachi1993, p. 67ff].
Similar existence results for embeddings 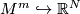 are valid also in the categories of real analytic maps and of isometrics (Nash) when
are valid also in the categories of real analytic maps and of isometrics (Nash) when 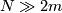 is sufficiently high.
is sufficiently high.
3 Classification
In order to get a survey of all ``essentially distinct´´ embeddings 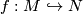 it is meaningful to introduce equivalence relations such as (ambient) isotopy, concordance, bordism etc., and to aim at classifying embeddings accordingly. Already for the most basic choices of
it is meaningful to introduce equivalence relations such as (ambient) isotopy, concordance, bordism etc., and to aim at classifying embeddings accordingly. Already for the most basic choices of  and
and  this may turn out to be a very difficult task. E.g. in the theory of knots (or links) where
this may turn out to be a very difficult task. E.g. in the theory of knots (or links) where  is a sphere (or a finite union of spheres) and
is a sphere (or a finite union of spheres) and 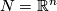 the multitude of possible knotting and linking phenomena is just overwhelming. Even classifying links up to the very crude equivalence relation `link homotopy´ is very far from having been achieved yet.
the multitude of possible knotting and linking phenomena is just overwhelming. Even classifying links up to the very crude equivalence relation `link homotopy´ is very far from having been achieved yet.
4 References
- [Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
- [Penrose&Whitehead&Zeeman1961] R. Penrose, J. Whitehead and E. Zeeman, Imbedding of manifolds in Euclidean space., Ann. of Math. 73 (1961) 613–623. MR0124909 (23 #A2218) Zbl 0113.38101
- [Rourke&Sanderson1972a] C. P. Rourke and B. J. Sanderson, Introduction to piecewise-linear topology, Springer-Verlag, 1972. MR0350744 (50 #3236) Zbl 0477.57003
- [Whitney1944] H. Whitney, The self-intersections of a smooth
 -manifold in
-manifold in  -space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237
-space, Ann. of Math. (2) 45 (1944), 220–246. MR0010274 (5,273g) Zbl 0063.08237
5 External links
- The Wikipedia page about embeddings
Theorem 7.1. We have $f \colon X \to Y$
Reference 7.1
By Theorem
{{#addlabel: test}}
Theorem 7.2. Frog
1 \ref{eqtest}
Here is some text leading up to an equation
7.3. $$ A = B $$
Here is some more text after the equation to see how it looks.
Here is some text leading up to an equation $$ A = B $$ Here is some more text after the equation to see how it looks.
4k 8 12 16 20 24 28 32 order bP4k 22.7 25.31 26.127 29.511 210.2047.691 213.8191 214.16384.3617
k 1 2 3 4 5 6 7 8 Bk 1/6 1/30 1/42 1/30 5/66 691/2730 7/6 3617/510
Dim n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 order Θn 1 1 1 1 1 1 28 2 8 6 992 1 3 2 16256 2 16 16 523264 24 bPn+1 1 1 1 1 1 1 28 1 2 1 992 1 1 1 8128 1 2 1 261632 1 Θn/bPn+1 1 1 1 1 1 1 1 2 2×2 6 1 1 3 2 2 2 2×2×2 8×2 2 24 πnS/J 1 2 1 1 1 2 1 2 2×2 6 1 1 3 2×2 2 2 2×2×2 8×2 2 24 index - 2 - - - 2 - - - - - - - 2 - - - - - -
$$ f \colon X \to Y $$
Extension DPL (warning): current configuration allows execution of DPL code from protected pages only.
Just a fest $f \colon A \to B$.
$\Q$
a theorem 7.4.
$\text{Spin}$
by theorem 7.4
- Amsterdam
- Rotterdam
- The Hague
[Mess1990]
$\left( \begin{array}{ll} \alpha & \beta \\ \gamma & \delta \end{array} \right)$
$f = T$
$ f : X \to Y$
$$ f : X \to Y $$
$\Ker$
$\mathscr{A}$ $\mathscr{B}$
bold italic emphasis
</wikitex>
6 Tests
[Ranicki1981] [Milnor1956] [Milnor1956, Theorem 1] [Milnor1956] [Milnor1956, Theorem 1] Frog
Proof.

7 Section
7.1 Subsection
Refert to subsection 9.1
Theorem 9.1. test
Refer to theorem 9.1
8 Section
An inter-Wiki link.
Another [1]; inter-Wiki link.
dfa[2]