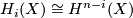|
|
| Line 1: |
Line 1: |
| − | <wikitex refresh>;
| + | Write here... |
| − | * For the more general case where $A H_1(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| + | |
| − | </wikitex>
| + | |
| − | <wikitex refresh include="MediaWiki:MathFontCM">;
| + | |
| − | * For the more general case where $B H_1(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| + | |
| − | </wikitex>
| + | |
| − | <wikitex refresh include="MediaWiki:MathFontHV">;
| + | |
| − | * For the more general case where $C H_1(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| + | |
| − | </wikitex>
| + | |
| − | <wikitex refresh include="MediaWiki:MathFont">;
| + | |
| − | * For the more general case where $E H_1(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| + | |
| − | </wikitex>
| + | |
| − | <wikitex refresh include="MediaWiki:MathFontLM">;
| + | |
| − | * For the more general case where $F H_1(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| + | |
| − | </wikitex>
| + | |
| − | == Introduction ==
| + | |
| | | | |
| − | <wikitex refresh include = "TexInclude:Sandbox; MediaWiki:MathFontCM">;
| |
| − | $\ZZZ$
| |
| − | $$ f = g$$
| |
| − | \ref{test}
| |
| − | Let $\mathcal{M}_6(0)$ be the set of diffeomorphism classes of [[wikipedia:Closed_manifold|closed]] [[wikipedia:Differentiable_manifold|smooth]] [[wikipedia:Simply-connected|simply-connected]] 2-connected 6-manifolds $M$.
| |
| − |
| |
| − | The classification $\mathcal{M}_6(0)$ was one of Smale's first applications of the [[Wikipedia:h-cobordism_theorem|h-cobordism]] theorem {{cite|Smale1962a|Corollary 1.3}}. The classification, as for [[Surface|oriented surfaces]] is strikingly simple: every 2-connected 6-manifold $M$ is diffeomorphic to a [[Wikipedia:Connected-sum|connected-sum]]
| |
| − | $$ M \cong \sharp_r(S^3 \times S^3)$$
| |
| − | where by definition $\sharp_0(S^3 \times S^3) = S^6$ and in general $r$ is determined by the formula for the [[Wikipedia:Euler characteristic|Euler characteristic]] of $M$
| |
| − | $$ \chi(M) = 2 - 2r.$$
| |
| − | * For the more general case where $H_2(M) \neq 0$, see [[6-manifolds: 1-connected|6-manifolds: 1-connected]].
| |
| − | </wikitex>
| |
| − |
| |
| − | <wikitex refresh include="MediaWiki:MathFontCM">;
| |
| − | == Construction and examples $L^2$ ==
| |
| − | The following gives a complete list of 2-connected 6-manifolds up to diffeomorphism:
| |
| − | * $S^6$, the standard 6-sphere.
| |
| − | * $\sharp_b(S^3 \times S^3)$, the $b$-fold connected sum of $S^3 \times S^3$.
| |
| − | </wikitex>
| |
| − |
| |
| − | == Invariants ==
| |
| − | <wikitex refresh include="MediaWiki:MathFontHV">;
| |
| − | Suppose that $M$ is diffeomorphic to $\sharp_b(S^3 \times S^3)$ then:
| |
| − | * $\pi_3(M) \cong H_3(M) \cong \Zz^{2b}$,
| |
| − | * the third Betti-number of $M$ is given by $b_3(M) = 2b$,
| |
| − | * the Euler characteristic of $M$ is given by $\chi(M) = 2 - 2b$,
| |
| − | * the [[Intersection forms|intersection form]] of $M$ is isomorphic to the sum of b-copies of $H_{-}(\Zz)$, the standard skew-symmetric hyperbolic form on $\Zz^2$.
| |
| − | </wikitex>
| |
| − |
| |
| − | <wikitex>
| |
| − | == Classification ==
| |
| − | Recall that the following theorem was stated in other words in the introduction:
| |
| − | {{beginthm|Theorem|{{cite|Smale1962a|Corolary 1.3}}}} \label{thm:classification}
| |
| − | The semi-group of 2-connected 6-manifolds is generated by $S^3 \times S^3$.
| |
| − | {{endthm}}
| |
| − | Hence if $\Nn$ denotes the natural numbers we obtain a bijection
| |
| − | $$ \mathcal{M}_6(0)\equiv \Nn,[M] \mapsto \frac{1}{2}b_3(M).$$
| |
| − | </wikitex>
| |
| − |
| |
| − | == Further discussion ==
| |
| − | === Topological 2-connected 6-manifolds ===
| |
| | <wikitex>; | | <wikitex>; |
| − | Let $\mathcal{M}^{\Top}_6(e)$ be the set of homeomorphism classes of topological 2-connected 6-manifolds.
| + | Poincare complexes are great: |
| − | {{beginthm|Theorem}}\label{test}
| + | $$ H_i(X) \cong H^{n-i}(X)$$ |
| − | Every topological 2-connected 6-manifold admits a smooth structure which is unique up to diffoemorphism. That is, there is a bijection
| + | |
| − | $$ \mathcal{M}_6(e) \rightarrow \mathcal{M}^{\Top}_6(e).$$ | + | |
| − | {{endthm}}
| + | |
| − | | + | |
| − | {{beginproof}}
| + | |
| − | For any such manifold $M$ we have $H^4(M; \Zz/2) \cong 0$ and so $M$ is smoothable (see [[6-manifolds: 1-connected#Smoothing theory|6-manifolds: 1-connected]]). Any two homeomorphic manifolds have the same Euler Characteristic and so by Theorem \ref{thm:classification} are diffeomorphic.
| + | |
| − | {{endproof}}
| + | |
| − | <wikitex>;
| + | |
| − | | + | |
| − | === Mapping class groups ===
| + | |
| − | ...
| + | |
| | </wikitex> | | </wikitex> |
| − |
| |
| − | == References ==
| |
| − | {{#RefList:}}
| |
Write here...