Regular homotopy group of immersions (Ex)
The goal of this exercise is to get more feeling for the regular homotopy group of  -immersions in
-immersions in  ,
, 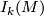 and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
Definition 0.1.
In [Lück2001] the group is defined as follows. Elements of 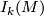 are represented by pointed
are represented by pointed  -immersions, i.e pairs
-immersions, i.e pairs 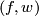 with
with 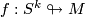 is an immersion which does not necessarily map the basepoint
is an immersion which does not necessarily map the basepoint 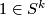 to the basepoint
to the basepoint 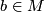 and
and 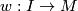 is a path from
is a path from  to
to 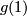 . Two pairs
. Two pairs 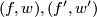 are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy
are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy 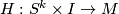 between
between  and
and  such that
such that 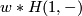 and
and 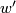 are homotopic relative endpoints. The sum of
are homotopic relative endpoints. The sum of ![[(f_0,w_0)]](/images/math/e/3/b/e3bf56b9cc42d5fa1a436a332645e6b7.png) and
and ![[(f_1,w_1)]](/images/math/d/8/7/d8744165e033e5253e9a649926775034.png) is defined by forming the (class of the) connected sum immersion
is defined by forming the (class of the) connected sum immersion 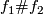 along with the (class of the) path
along with the (class of the) path 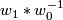 . The action of
. The action of 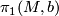 is given by mapping
is given by mapping ![[(f,w)]](/images/math/0/e/1/0e112364461ebcc7e6f38af22065e04c.png) to
to ![[(f,w\ast\omega)]](/images/math/5/6/3/563d4451613a70f3210af25abc426b30.png) where
where 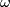 is a loop at
is a loop at  representing a
representing a 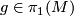 .
.
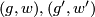 is described as follows. Choose representavives with
is described as follows. Choose representavives with 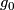 and
and 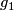 transverse. For every double point
transverse. For every double point 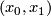 with
with 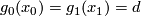 determine the sign
determine the sign 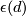 in the usual way, i.e. by comparing orientations of
in the usual way, i.e. by comparing orientations of 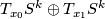 and
and 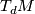 . The element
. The element 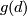 is given by the class of the loop
is given by the class of the loop 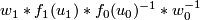
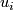 is a path in
is a path in 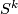 from
from  to
to 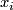 .
.
Definition 0.2.
In [Ranicki2002] the group is defined as follows. Elements of 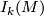 are represented by
are represented by 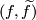 with
with 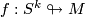 a
a  -immersion and
-immersion and 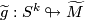 a lift of
a lift of  to the universal cover of
to the universal cover of  . Two pairs
. Two pairs 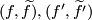 are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of
are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of 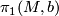 is via deck transformations on the lift.
is via deck transformations on the lift.
To determine the equivariant intersection of 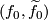 and
and 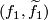 choose
choose  and
and  to be transverse. For every doublepoint
to be transverse. For every doublepoint 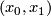 with
with 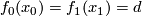 there exists an element
there exists an element 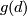 such that
such that 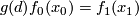 . Define the equivariant index of
. Define the equivariant index of  and
and  at
at  to be
to be 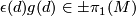 where
where 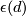 is determined by comparing orientations again.
is determined by comparing orientations again.
1) Show that the above definitions of ![\mathbb{Z}[\pi_1(M)]](/images/math/9/0/4/904f46e21f958c042af4c7df4637c0b1.png) -modules are equivalent.
-modules are equivalent.
2) Show that the descriptions of the equivariant intersections of (regular homotopy classes of)  -immersions coincide.
-immersions coincide.
3) Show that the corresponding descriptions of Wall's 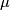 -form (the self-intersection form) coincide up to possible conjugation by a fixed element
-form (the self-intersection form) coincide up to possible conjugation by a fixed element 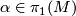 .
.
 ,
, 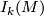 and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
Definition 0.1.
In [Lück2001] the group is defined as follows. Elements of 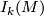 are represented by pointed
are represented by pointed  -immersions, i.e pairs
-immersions, i.e pairs 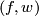 with
with 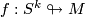 is an immersion which does not necessarily map the basepoint
is an immersion which does not necessarily map the basepoint 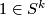 to the basepoint
to the basepoint 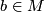 and
and 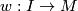 is a path from
is a path from  to
to 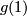 . Two pairs
. Two pairs 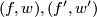 are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy
are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy 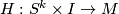 between
between  and
and  such that
such that 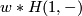 and
and 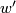 are homotopic relative endpoints. The sum of
are homotopic relative endpoints. The sum of ![[(f_0,w_0)]](/images/math/e/3/b/e3bf56b9cc42d5fa1a436a332645e6b7.png) and
and ![[(f_1,w_1)]](/images/math/d/8/7/d8744165e033e5253e9a649926775034.png) is defined by forming the (class of the) connected sum immersion
is defined by forming the (class of the) connected sum immersion 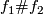 along with the (class of the) path
along with the (class of the) path 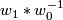 . The action of
. The action of 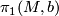 is given by mapping
is given by mapping ![[(f,w)]](/images/math/0/e/1/0e112364461ebcc7e6f38af22065e04c.png) to
to ![[(f,w\ast\omega)]](/images/math/5/6/3/563d4451613a70f3210af25abc426b30.png) where
where 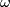 is a loop at
is a loop at  representing a
representing a 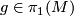 .
.
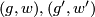 is described as follows. Choose representavives with
is described as follows. Choose representavives with 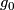 and
and 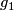 transverse. For every double point
transverse. For every double point 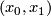 with
with 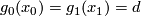 determine the sign
determine the sign 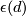 in the usual way, i.e. by comparing orientations of
in the usual way, i.e. by comparing orientations of 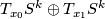 and
and 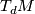 . The element
. The element 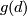 is given by the class of the loop
is given by the class of the loop 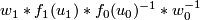
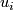 is a path in
is a path in 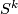 from
from  to
to 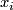 .
.
Definition 0.2.
In [Ranicki2002] the group is defined as follows. Elements of 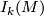 are represented by
are represented by 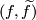 with
with 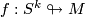 a
a  -immersion and
-immersion and 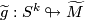 a lift of
a lift of  to the universal cover of
to the universal cover of  . Two pairs
. Two pairs 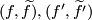 are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of
are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of 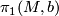 is via deck transformations on the lift.
is via deck transformations on the lift.
To determine the equivariant intersection of 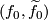 and
and 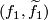 choose
choose  and
and  to be transverse. For every doublepoint
to be transverse. For every doublepoint 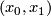 with
with 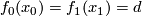 there exists an element
there exists an element 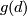 such that
such that 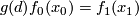 . Define the equivariant index of
. Define the equivariant index of  and
and  at
at  to be
to be 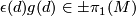 where
where 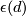 is determined by comparing orientations again.
is determined by comparing orientations again.
1) Show that the above definitions of ![\mathbb{Z}[\pi_1(M)]](/images/math/9/0/4/904f46e21f958c042af4c7df4637c0b1.png) -modules are equivalent.
-modules are equivalent.
2) Show that the descriptions of the equivariant intersections of (regular homotopy classes of)  -immersions coincide.
-immersions coincide.
3) Show that the corresponding descriptions of Wall's 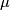 -form (the self-intersection form) coincide up to possible conjugation by a fixed element
-form (the self-intersection form) coincide up to possible conjugation by a fixed element 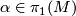 .
.
 ,
, 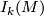 and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
and the intersection/self-intersection form on it. Below are two definitions of it. Both are used in [Wall1999].
Definition 0.1.
In [Lück2001] the group is defined as follows. Elements of 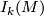 are represented by pointed
are represented by pointed  -immersions, i.e pairs
-immersions, i.e pairs 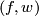 with
with 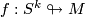 is an immersion which does not necessarily map the basepoint
is an immersion which does not necessarily map the basepoint 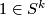 to the basepoint
to the basepoint 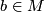 and
and 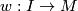 is a path from
is a path from  to
to 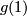 . Two pairs
. Two pairs 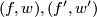 are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy
are considered equivalent if they are pointed homotopic, i.e. if there exists a regular homotopy 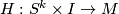 between
between  and
and  such that
such that 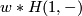 and
and 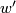 are homotopic relative endpoints. The sum of
are homotopic relative endpoints. The sum of ![[(f_0,w_0)]](/images/math/e/3/b/e3bf56b9cc42d5fa1a436a332645e6b7.png) and
and ![[(f_1,w_1)]](/images/math/d/8/7/d8744165e033e5253e9a649926775034.png) is defined by forming the (class of the) connected sum immersion
is defined by forming the (class of the) connected sum immersion 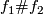 along with the (class of the) path
along with the (class of the) path 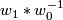 . The action of
. The action of 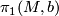 is given by mapping
is given by mapping ![[(f,w)]](/images/math/0/e/1/0e112364461ebcc7e6f38af22065e04c.png) to
to ![[(f,w\ast\omega)]](/images/math/5/6/3/563d4451613a70f3210af25abc426b30.png) where
where 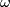 is a loop at
is a loop at  representing a
representing a 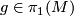 .
.
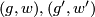 is described as follows. Choose representavives with
is described as follows. Choose representavives with 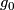 and
and 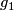 transverse. For every double point
transverse. For every double point 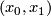 with
with 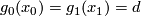 determine the sign
determine the sign 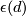 in the usual way, i.e. by comparing orientations of
in the usual way, i.e. by comparing orientations of 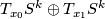 and
and 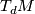 . The element
. The element 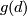 is given by the class of the loop
is given by the class of the loop 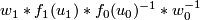
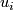 is a path in
is a path in 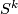 from
from  to
to 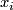 .
.
Definition 0.2.
In [Ranicki2002] the group is defined as follows. Elements of 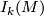 are represented by
are represented by 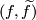 with
with 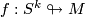 a
a  -immersion and
-immersion and 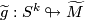 a lift of
a lift of  to the universal cover of
to the universal cover of  . Two pairs
. Two pairs 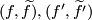 are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of
are considered equivalent if they are regular homotopy equivalent. The sum is given by connected sum. The action of 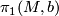 is via deck transformations on the lift.
is via deck transformations on the lift.
To determine the equivariant intersection of 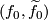 and
and 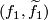 choose
choose  and
and  to be transverse. For every doublepoint
to be transverse. For every doublepoint 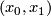 with
with 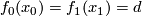 there exists an element
there exists an element 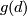 such that
such that 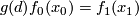 . Define the equivariant index of
. Define the equivariant index of  and
and  at
at  to be
to be 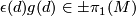 where
where 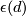 is determined by comparing orientations again.
is determined by comparing orientations again.
1) Show that the above definitions of ![\mathbb{Z}[\pi_1(M)]](/images/math/9/0/4/904f46e21f958c042af4c7df4637c0b1.png) -modules are equivalent.
-modules are equivalent.
2) Show that the descriptions of the equivariant intersections of (regular homotopy classes of)  -immersions coincide.
-immersions coincide.
3) Show that the corresponding descriptions of Wall's 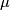 -form (the self-intersection form) coincide up to possible conjugation by a fixed element
-form (the self-intersection form) coincide up to possible conjugation by a fixed element 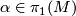 .
.