Questions about surgery theory
This page organizes questions and answers about surgery theory.
The natural first port of call for quick answers is Mathoverflow.
Below is a list of questions, possibly with answers.
The Atlas also has a chapter Questions for questions which attract longer answers.
Contents |
1 Questions
1.1 How can you tell if a space is homotopy equivalent to a manifold?
This is in fact a Mathoverflow question.
1.2 Simply connected surgery obstruction groups
How does one prove that
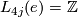 ,
, 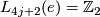 and
and 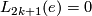 ?
?
Read [Kervaire&Milnor1963] and/or [Browder1972] and/or [Ranicki2002, Chapter 12].
1.3 CW structures on topological 4-manifolds
Do topological 4-manifolds have a 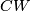 structure?
structure?
Topological manifolds of dimension 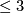 have a piecewise linear (in fact a differentiable)
structure ([Moise1952]), and a fortiori are triangulable. Topological manifolds of dimension
have a piecewise linear (in fact a differentiable)
structure ([Moise1952]), and a fortiori are triangulable. Topological manifolds of dimension
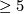 have a handlebody structure ([Kirby&Siebenmann1977]), and hence a
have a handlebody structure ([Kirby&Siebenmann1977]), and hence a 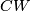 structure.
All topological manifolds in dimensions
structure.
All topological manifolds in dimensions 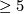 can be triangulated if and only if the Kervaire-Milnor-Rohlin
surjection
can be triangulated if and only if the Kervaire-Milnor-Rohlin
surjection 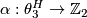 splits ([Galewski&Stern1980]). There do exist non-triangulable
topological 4-manifolds, e.g. the Freedman
splits ([Galewski&Stern1980]). There do exist non-triangulable
topological 4-manifolds, e.g. the Freedman 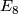 -manifold ([Akbulut&McCarthy1990]).
-manifold ([Akbulut&McCarthy1990]).
2 References
- [Akbulut&McCarthy1990] S. Akbulut and J. D. McCarthy, Casson's invariant for oriented homology
 -spheres, Princeton University Press, Princeton, NJ, 1990. MR1030042 (90k:57017) Zbl 0695.57011
-spheres, Princeton University Press, Princeton, NJ, 1990. MR1030042 (90k:57017) Zbl 0695.57011
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Galewski&Stern1980] D. E. Galewski and R. J. Stern, Classification of simplicial triangulations of topological manifolds, Ann. of Math. (2) 111 (1980), no.1, 1–34. MR558395 (81f:57012) Zbl 0441.57017
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Moise1952] E. E. Moise, Affine structures in
 -manifolds. V. The triangulation theorem and Hauptvermutung, Ann. of Math. (2) 56 (1952), 96–114. MR0048805 (14,72d) Zbl 0048.17102
-manifolds. V. The triangulation theorem and Hauptvermutung, Ann. of Math. (2) 56 (1952), 96–114. MR0048805 (14,72d) Zbl 0048.17102
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001