Questions about surgery theory
(Difference between revisions)
(→Questions) |
|||
| Line 8: | Line 8: | ||
== Questions == | == Questions == | ||
| + | === How do I tell if a space is homotopy equivalent to a manifold? === | ||
| + | |||
| + | This is in fact a [http://mathoverflow.net/questions/129/how-can-you-tell-if-a-space-is-homotopy-equivalent-to-a-manifold Mathoverflow question]. | ||
| + | |||
=== Simply connected odd-dimensional L-groups === | === Simply connected odd-dimensional L-groups === | ||
<wikitex>; | <wikitex>; | ||
Revision as of 19:31, 6 August 2010
This page organizes questions and answers about surgery theory.
The natural first port of call for quick answers is Mathoverflow.
Below is a list of questions, possibly with answers.
The Atlas also has a chapter Questions for questions which attract longer answers.
Contents |
1 Questions
1.1 How do I tell if a space is homotopy equivalent to a manifold?
This is in fact a Mathoverflow question.
1.2 Simply connected odd-dimensional L-groups
How does one prove that 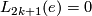 ?
?
Read [Kervaire&Milnor1963, Section 6] and/or [Browder1972, IV.3] and/or [Ranicki2002, 12.6].
2 References
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001