Questions about surgery theory
Alreadydone (Talk | contribs) |
m (→Handlebody and CW structures on topological 4-manifolds) |
||
| (One intermediate revision by one user not shown) | |||
| Line 34: | Line 34: | ||
cannot have a handlebody structure. | cannot have a handlebody structure. | ||
| − | According Allen Hatcher's Algebraic Topology (starting from Corollary A.12), A compact manifold is homotopy equivalent to a CW complex. Restricting to closed manifolds: "for manifolds of dimensions less than 4, simplicial complex structures always exist. In dimension 4 there are closed manifolds that do not have simplicial complex structures, while the existence of CW structures is an open question. In dimensions greater than 4, CW structures always exist, but whether simplicial structures always exist is unknown, though it is known that there are n-manifolds not having simplicial structures locally isomorphic to any linear simplicial subdivision of | + | According Allen Hatcher's Algebraic Topology (starting from Corollary A.12), A compact manifold is homotopy equivalent to a CW complex. Restricting to closed manifolds: "for manifolds of dimensions less than 4, simplicial complex structures always exist. In dimension 4 there are closed manifolds that do not have simplicial complex structures, while the existence of CW structures is an open question. In dimensions greater than 4, CW structures always exist, but whether simplicial structures always exist is unknown, though it is known that there are n-manifolds not having simplicial structures locally isomorphic to any linear simplicial subdivision of $\Rr^n$, for all $n \geq 4$. For more on these questions, see {{cite|Kirby&Siebenmann1977}} and {{cite|Freedman&Quinn1990}}." |
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
Latest revision as of 15:35, 7 February 2012
This page organizes questions and answers about surgery theory.
The natural first port of call for quick answers is Mathoverflow.
Below is a list of questions, possibly with answers.
The Atlas also has a chapter Questions for questions which attract longer answers.
Contents |
[edit] 1 Questions
[edit] 1.1 How can you tell if a space is homotopy equivalent to a manifold?
This is in fact a Mathoverflow question.
[edit] 1.2 Simply connected surgery obstruction groups
How does one prove that
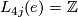 ,
, 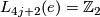 and
and 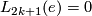 ?
?
Read [Kervaire&Milnor1963] and/or [Browder1972] and/or [Ranicki2002, Chapter 12].
[edit] 1.3 Handlebody and CW structures on topological 4-manifolds
Do topological 4-manifolds have a handlebody structrure? a  structure?
structure?
Topological manifolds of dimension 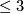 have a piecewise linear (in fact a differentiable)
structure ([Moise1952]), and a fortiori are triangulable. Topological manifolds of dimension
have a piecewise linear (in fact a differentiable)
structure ([Moise1952]), and a fortiori are triangulable. Topological manifolds of dimension
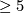 have a handlebody structure ([Kirby&Siebenmann1977]), and hence a
have a handlebody structure ([Kirby&Siebenmann1977]), and hence a  structure.
All topological manifolds in dimensions
structure.
All topological manifolds in dimensions 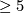 can be triangulated if and only if the Kervaire-Milnor-Rohlin
surjection
can be triangulated if and only if the Kervaire-Milnor-Rohlin
surjection 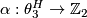 splits ([Galewski&Stern1980]). There do exist non-triangulable
topological 4-manifolds, e.g. the Freedman
splits ([Galewski&Stern1980]). There do exist non-triangulable
topological 4-manifolds, e.g. the Freedman 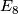 -manifold ([Akbulut&McCarthy1990]).
-manifold ([Akbulut&McCarthy1990]).
Rob Kirby's answer to the handlebody question (28.8.2010): If a TOP handle decomposition, then the first 1-handle attached to a (smooth) 0-handle can be isotoped to have a smooth attaching map, so the result is smooth. Just keep going like this, using the fact that a top embedding of the attaching sphere can be smoothed in dim 3, and the result is a smooth 4-mfd. Some aren't!!! So a nonsmoothable 4-manifold, e.g. the Freedman 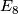 -manifold,
cannot have a handlebody structure.
-manifold,
cannot have a handlebody structure.
According Allen Hatcher's Algebraic Topology (starting from Corollary A.12), A compact manifold is homotopy equivalent to a CW complex. Restricting to closed manifolds: "for manifolds of dimensions less than 4, simplicial complex structures always exist. In dimension 4 there are closed manifolds that do not have simplicial complex structures, while the existence of CW structures is an open question. In dimensions greater than 4, CW structures always exist, but whether simplicial structures always exist is unknown, though it is known that there are n-manifolds not having simplicial structures locally isomorphic to any linear simplicial subdivision of  , for all
, for all 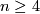 . For more on these questions, see [Kirby&Siebenmann1977] and [Freedman&Quinn1990]."
. For more on these questions, see [Kirby&Siebenmann1977] and [Freedman&Quinn1990]."
[edit] 2 References
- [Akbulut&McCarthy1990] S. Akbulut and J. D. McCarthy, Casson's invariant for oriented homology
 -spheres, Princeton University Press, Princeton, NJ, 1990. MR1030042 (90k:57017) Zbl 0695.57011
-spheres, Princeton University Press, Princeton, NJ, 1990. MR1030042 (90k:57017) Zbl 0695.57011
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Freedman&Quinn1990] M. H. Freedman and F. Quinn, Topology of 4-manifolds, Princeton University Press, Princeton, NJ, 1990. MR1201584 (94b:57021) Zbl 0705.57001
- [Galewski&Stern1980] D. E. Galewski and R. J. Stern, Classification of simplicial triangulations of topological manifolds, Ann. of Math. (2) 111 (1980), no.1, 1–34. MR558395 (81f:57012) Zbl 0441.57017
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Moise1952] E. E. Moise, Affine structures in
 -manifolds. V. The triangulation theorem and Hauptvermutung, Ann. of Math. (2) 56 (1952), 96–114. MR0048805 (14,72d) Zbl 0048.17102
-manifolds. V. The triangulation theorem and Hauptvermutung, Ann. of Math. (2) 56 (1952), 96–114. MR0048805 (14,72d) Zbl 0048.17102
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001