Questions about surgery theory
(Difference between revisions)
(→Simply connected odd-dimensional L-groups) |
(→Simply connected odd-dimensional L-groups) |
||
| Line 11: | Line 11: | ||
How does one prove that $L_{2k+1}(e) = 0$ ? | How does one prove that $L_{2k+1}(e) = 0$ ? | ||
| − | Read | + | Read {{cite|Kervaire&Milnor1963|Section 6}} and/or {{cite|Browder1972|Iv.3}} and/or {{cite|Ranicki2002|12.6}}. |
</wikitex> | </wikitex> | ||
Revision as of 15:43, 6 August 2010
This page organizes questions and answers about surgery theory.
The natural first port of call for quick answers is [Mathoverflow].
Below you find a list of question pages and proposed questions pages: each question in the Atlas has its own page in the chapter.
Contents |
1 Questions
1.1 Simply connected odd-dimensional L-groups
How does one prove that 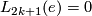 ?
?
Read [Kervaire&Milnor1963, Section 6] and/or [Browder1972, Iv.3] and/or [Ranicki2002, 12.6].
2 References
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001