Pin structures
| Line 25: | Line 25: | ||
The obstruction for existence of a $Pin^+$-structure on $M$ is the characteristic class $w_2(M)$. | The obstruction for existence of a $Pin^+$-structure on $M$ is the characteristic class $w_2(M)$. | ||
| − | If $M$ does admit $Pin$ structures, then the set of isomorphism classes of $Pin^+$-structures on $M$ is | + | If $M$ does admit $Pin$ structures, then the set of isomorphism classes of $Pin^+$-structures on $M$ is acted upon freely |
| + | and transitively by $H^1(M;\Zz_2)$. | ||
The obstruction for existence of a $Pin^-$-structure on $M$ is the characteristic class $w_2(M)+w_1(M)^2$. | The obstruction for existence of a $Pin^-$-structure on $M$ is the characteristic class $w_2(M)+w_1(M)^2$. | ||
| − | If $M$ does admit $Pin$ structures, then the set of isomorphism classes of $Pin^-$-structures on $M$ is | + | If $M$ does admit $Pin$ structures, then the set of isomorphism classes of $Pin^-$-structures on $M$ is acted upon freely |
| − | + | and transitively by $H^1(M;\Zz_2)$. | |
A $Pin^\pm$-structure together with an orientation is equivalent to a $Spin$-structure. | A $Pin^\pm$-structure together with an orientation is equivalent to a $Spin$-structure. | ||
Revision as of 11:16, 1 April 2011
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
For an oriented manifold a spin structure is a reduction of the structure group of its
tangent bundle from the connected topological group  to the double (universal) cover
to the double (universal) cover  .
The non-connected group
.
The non-connected group  has two nontrivial central extensions (double covers) by
has two nontrivial central extensions (double covers) by  with different group structures, denoted by
with different group structures, denoted by 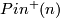 and
and 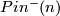 .
A
.
A 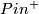 -structure on a manifold is thus a a reduction of the structure group of its tangent bundle
from
-structure on a manifold is thus a a reduction of the structure group of its tangent bundle
from  to
to 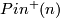 , and similarly for
, and similarly for 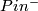 -structures.
-structures.
A 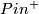 -structure on
-structure on  is equivalent to a
is equivalent to a 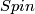 -structure on
-structure on 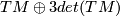 ,
a
,
a 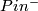 -structure on
-structure on  is equivalent to a
is equivalent to a 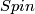 -structure on
-structure on 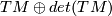 .
.
The obstruction for existence of a 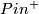 -structure on
-structure on  is the characteristic class
is the characteristic class 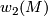 .
If
.
If  does admit
does admit 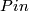 structures, then the set of isomorphism classes of
structures, then the set of isomorphism classes of 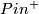 -structures on
-structures on  is acted upon freely
and transitively by
is acted upon freely
and transitively by 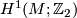 .
.
The obstruction for existence of a 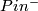 -structure on
-structure on  is the characteristic class
is the characteristic class 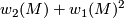 .
If
.
If  does admit
does admit 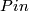 structures, then the set of isomorphism classes of
structures, then the set of isomorphism classes of 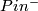 -structures on
-structures on  is acted upon freely
and transitively by
is acted upon freely
and transitively by 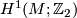 .
.
A 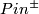 -structure together with an orientation is equivalent to a
-structure together with an orientation is equivalent to a 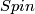 -structure.
-structure.
For more information on 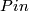 -manifolds, including a computation of the low-dimensional bordism groups
of
-manifolds, including a computation of the low-dimensional bordism groups
of 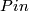 -manifolds, see [Kirby&Taylor1990].
-manifolds, see [Kirby&Taylor1990].
2 Examples
For 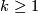 :
:
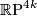 admits two
admits two 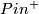 -structures and no
-structures and no 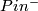 -structure.
-structure.
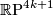 admits no
admits no 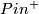 -structure and no
-structure and no 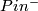 -structure.
-structure.
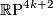 admits no
admits no 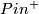 -structure and two
-structure and two 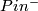 -structures.
-structures.
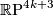 admits two
admits two 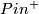 -structures and two
-structures and two 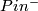 -structures.
-structures.
3 References
- [Kirby&Taylor1990] R. C. Kirby and L. R. Taylor,
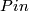 structures on low-dimensional manifolds, Geometry of low-dimensional manifolds, 2 (Durham, 1989), Cambridge Univ. Press (1990), 177–242. MR1171915 (94b:57031) Zbl 0754.57020
structures on low-dimensional manifolds, Geometry of low-dimensional manifolds, 2 (Durham, 1989), Cambridge Univ. Press (1990), 177–242. MR1171915 (94b:57031) Zbl 0754.57020