Petrie conjecture
(→Further discussion) |
(→Further discussion) |
||
| Line 37: | Line 37: | ||
A symplectic version of the Petrie conjecture is discussed by Tolman {{cite|Tolman2010}}. In particular, the following question has been posed. | A symplectic version of the Petrie conjecture is discussed by Tolman {{cite|Tolman2010}}. In particular, the following question has been posed. | ||
{{beginthm|Question}} | {{beginthm|Question}} | ||
| − | If the circle $S^1$ acts in a Hamiltonian way on a compact symplectic manifold $M$ with $H^{2i}(M; \mathbb{R}) \cong H^{2i}(\mathbb{C}P^n; \mathbb{R})$ for all $i$, | + | If the circle $S^1$ acts in a Hamiltonian way on a compact symplectic manifold $M$ with $H^{2i}(M; \mathbb{R}) \cong H^{2i}(\mathbb{C}P^n; \mathbb{R})$ for all $i \geq 0$, |
| − | is it true that $H^{j}(M; \mathbb{Z}) \cong H^{j}(\mathbb{C}P^n; \mathbb{Z})$ for all $j$? Is the total Chern class of $M$ determined by the cohomology ring $H^*(M;\mathbb{Z})$? | + | is it true that $H^{j}(M; \mathbb{Z}) \cong H^{j}(\mathbb{C}P^n; \mathbb{Z})$ for all $j \geq 0$? Is the total Chern class of $M$ determined by the cohomology ring $H^*(M;\mathbb{Z})$? |
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
Revision as of 13:04, 16 December 2010
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Problem
If a compact Lie group  acts smoothly and non-trivially on a closed smooth manifold
acts smoothly and non-trivially on a closed smooth manifold  , what constraints does this place on the topology of
, what constraints does this place on the topology of  in general and on the Pontrjagin classes of
in general and on the Pontrjagin classes of  in particular?
In the case where
in particular?
In the case where  is homotopy equivalent to
is homotopy equivalent to 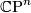 ,
, 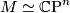 , Petrie [Petrie1972] restricted his attention to actions of the Lie group
, Petrie [Petrie1972] restricted his attention to actions of the Lie group
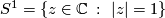 and proved that if the fixed point set of the action consists only of isolated fixed points, then the Pontrjagin classes of
and proved that if the fixed point set of the action consists only of isolated fixed points, then the Pontrjagin classes of  are determined by the representations of
are determined by the representations of  at the fixed points. Motivated by this result, Petrie [Petrie1972] posed the following conjecture.
at the fixed points. Motivated by this result, Petrie [Petrie1972] posed the following conjecture.
Conjecture 1.1 (Petrie conjecture).
Suppose that  acts smoothly and non-trivially on a closed smooth
acts smoothly and non-trivially on a closed smooth  -manifold
-manifold 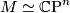 . Then the total Pontrjagin class
. Then the total Pontrjagin class 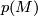 of
of  agrees with that of
agrees with that of 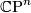 , i.e.,
, i.e.,
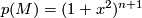 for a generator
for a generator  of
of 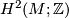 .
.
2 Progress to date
As of November 30, 2010, the Petrie conjecture has not been confirmed in general. However, it has been proven in the following special cases.
- Petrie [Petrie1973] has verified his conjecture under the assumption that the manifold
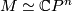 admits a smooth action of the torus
admits a smooth action of the torus 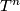 .
.
- By the work of [Dejter1976], the Petrie conjecture is true if
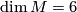 , i.e.,
, i.e., 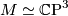 and hence, if
and hence, if 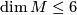 .
.
- Related results go back to [Musin1978] and [Musin1980], in particular, the latter work shows that the Petrie conjecture holds if
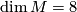 , i.e.,
, i.e., 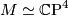 .
.
- According to [Hattori1978], the Petrie conjecture holds if
 admits an invariant almost complex structure with the first Chern class
admits an invariant almost complex structure with the first Chern class 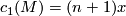 .
.
- Other special cases where the Petrie conjecture holds are described by [Wang1975], [Yoshida1975/76], [Iberkleid1978].
- By [Tsukada&Washiyama1979] and [Masuda1981], the Petrie conjecture is true if the fixed point set consists of three or four connected components.
- Masuda [Masuda1983] proved the Petrie conjecture in the case where
 admits a specific smooth action of
admits a specific smooth action of 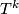 for
for 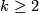 .
.
- The work of [James1985] confirms the result of [Musin1980] that the Petrie conjecture is true if
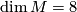 , i.e.,
, i.e., 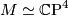 .
.
- According to [Dessai2002], the Petrie conjecture holds if
 admits an appropriate smooth action of
admits an appropriate smooth action of 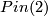 and
and 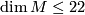 .
.
- It follows from [Dessai&Wilking2004] that the Petrie conjecture holds if
 admits a smooth action of
admits a smooth action of 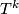 and
and 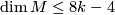 .
.
3 Further discussion
A related problem posed by Masuda and Suh [Masuda&Suh2008] reads as follows. For two toric  -manifolds with isomorphic cohomology rings, is there an isomorphism between the cohomology rings which preserves the Pontrjagin classes of the two manifolds? A stroger version of the question reads as follows.
-manifolds with isomorphic cohomology rings, is there an isomorphism between the cohomology rings which preserves the Pontrjagin classes of the two manifolds? A stroger version of the question reads as follows.
Question 3.1.
For two toric  -manifolds with isomorphic cohomology rings, is it true that any isomorphism between the cohomology rings preserves the Pontrjagin classes of the two manifolds?
-manifolds with isomorphic cohomology rings, is it true that any isomorphism between the cohomology rings preserves the Pontrjagin classes of the two manifolds?
A symplectic version of the Petrie conjecture is discussed by Tolman [Tolman2010]. In particular, the following question has been posed.
Question 3.2.
If the circle  acts in a Hamiltonian way on a compact symplectic manifold
acts in a Hamiltonian way on a compact symplectic manifold  with
with 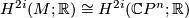 for all
for all 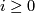 ,
is it true that
,
is it true that 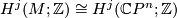 for all
for all 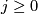 ? Is the total Chern class of
? Is the total Chern class of  determined by the cohomology ring
determined by the cohomology ring 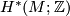 ?
?
4 References
- [Dejter1976] I. J. Dejter, Smooth
 -manifolds in the homotopy type of
-manifolds in the homotopy type of 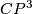 , Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
, Michigan Math. J. 23 (1976), no.1, 83–95. MR0402789 (53 #6603) Zbl 0326.57009
- [Dessai&Wilking2004] A. Dessai and B. Wilking, Torus actions on homotopy complex projective spaces, Math. Z. 247 (2004), no.3, 505–511. MR2114425 (2006c:57033) Zbl 1068.57034
- [Dessai2002] A. Dessai, Homotopy complex projective spaces with
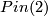 -action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
-action, Topology Appl. 122 (2002), no.3, 487–499. MR1911696 (2003f:58048) Zbl 0998.57048
- [Hattori1978] A. Hattori,
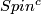 -structures and
-structures and  -actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
-actions, Invent. Math. 48 (1978), no.1, 7–31. MR508087 (80e:57051) Zbl 0395.57020
- [Iberkleid1978] W. Iberkleid, Pseudolinear spheres, Michigan Math. J. 25 (1978), no.3, 359–370. MR512906 (80d:57023) Zbl 0377.57008
- [James1985] D. M. James, Smooth
 actions on homotopy
actions on homotopy 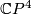 's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
's, Michigan Math. J. 32 (1985), no.3, 259–266. MR803831 (87c:57031) Zbl 0602.57026
- [Masuda&Suh2008] M. Masuda and D. Y. Suh, Classification problems of toric manifolds via topology, Toric topology, Amer. Math. Soc. (2008), 273–286. MR2428362 (2010d:14071) Zbl 1160.57032
- [Masuda1981] M. Masuda, On smooth
 -actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
-actions on cohomology complex projective spaces. The case where the fixed point set consists of four connected components, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), no.1, 127–167. MR617869 (82i:57031) Zbl 0462.57019
- [Masuda1983] M. Masuda, Integral weight system of torus actions on cohomology complex projective spaces, Japan. J. Math. (N.S.) 9 (1983), no.1, 55–86. MR722536 (84m:57027) Zbl 0531.57037
- [Musin1978] O. R. Musin, Unitary actions of
 on complex projective spaces, Uspekhi Mat. Nauk 33 (1978), no.6(204), 225–226. MR526030 (81a:57037)
on complex projective spaces, Uspekhi Mat. Nauk 33 (1978), no.6(204), 225–226. MR526030 (81a:57037)
- [Musin1980] O. R. Musin, Actions of the circle on homotopy complex projective spaces, Mat. Zametki 28 (1980), no.1, 139–152, 170. MR585071 (81m:57027)
- [Petrie1972] T. Petrie, Smooth
 -actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
-actions on homotopy complex projective spaces and related topics, Bull. Amer. Math. Soc. 78 (1972), 105–153. MR0296970 Zbl 0247.57010
- [Petrie1973] T. Petrie, Torus actions on homotopy complex projective spaces, Invent. Math. 20 (1973), 139–146. MR0322893 (48 #1254) Zbl 0262.57021
- [Tolman2010] S. Tolman, On a symplectic generalization of Petrie's conjecture, Trans. Amer. Math. Soc. 362 (2010), no.8, 3963–3996. MR2638879 Zbl 1216.53074
- [Tsukada&Washiyama1979] E. Tsukada and R. Washiyama,
 -actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
-actions on cohomology complex projective spaces with three components of the fixed point sets, Hiroshima Math. J. 9 (1979), no.1, 41–46. MR529325 (80j:57043) Zbl 0411.57037
- [Wang1975] K. Wang, Differentiable circle group actions on homotopy complex projective spaces, Math. Ann. 214 (1975), 73–80. MR0372895 (51 #9099) Zbl 0285.57025
- [Yoshida1975/76] T. Yoshida, On smooth semifree
 actions on cohomology complex projective spaces, Publ. Res. Inst. Math. Sci. 11 (1975/76), no.2, 483–496. MR0445528 (56 #3868) Zbl 0326.57008
actions on cohomology complex projective spaces, Publ. Res. Inst. Math. Sci. 11 (1975/76), no.2, 483–496. MR0445528 (56 #3868) Zbl 0326.57008