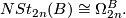Parametric connected sum
(→Parametric connected sum along k-spheres) |
|||
| Line 21: | Line 21: | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Connected sum along k-spheres == |
<wikitex>; | <wikitex>; | ||
We say above that to define connected sum for connected k-manifolds $M$ and $N$ it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreove, the disjoint union $D^n \sqcup D^n$ is the unique [[thickening]] of $S^0$. This motivates the following | We say above that to define connected sum for connected k-manifolds $M$ and $N$ it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreove, the disjoint union $D^n \sqcup D^n$ is the unique [[thickening]] of $S^0$. This motivates the following | ||
| Line 40: | Line 40: | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| + | |||
== Applications of k-sphere conneted sum == | == Applications of k-sphere conneted sum == | ||
<wikitex>; | <wikitex>; | ||
Revision as of 21:47, 3 March 2010
Contents |
1 Introduction
Parametric connected sum is an operation on compact connected n-manifolds  and
and  equipped with codimension 0-embeddings
equipped with codimension 0-embeddings 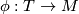 and
and 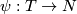 of a compact connected manifold
of a compact connected manifold  . It generalises the usual connected sum operation but is more subtle since the isotopy classes of the embeddings
. It generalises the usual connected sum operation but is more subtle since the isotopy classes of the embeddings 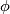 and
and 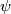 may be significantly more complicated than the isotopy classes of embeddings of n-discs need for connected sum: these last are determined by (local) orientations.
may be significantly more complicated than the isotopy classes of embeddings of n-discs need for connected sum: these last are determined by (local) orientations.
2 Connected sum
Let  be a compact connected n-manifold with base point
be a compact connected n-manifold with base point 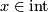 . Recall that that a local orientation for
. Recall that that a local orientation for  is a choice of orientation of
is a choice of orientation of 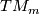 , the tangent space to
, the tangent space to  at
at  . We write
. We write 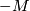 for
for  with the opposition orientation at
with the opposition orientation at  . Of course, if
. Of course, if  is orientable then a local orientation for
is orientable then a local orientation for  defines an orientation on
defines an orientation on  .
.
If  and
and  are locally oriented n-manifolds then their connected sum is defined by
are locally oriented n-manifolds then their connected sum is defined by
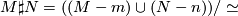
where 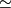 is defined using the local orientations to identify small balls about
is defined using the local orientations to identify small balls about  and
and  . The diffeomorphism type of
. The diffeomorphism type of 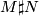 is well-defined: in fact
is well-defined: in fact 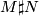 is the outcome of 0-surgery on
is the outcome of 0-surgery on 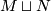 . The essential point is [Hirsch] which states, for any
. The essential point is [Hirsch] which states, for any  and any two compatibly oriented embeddings
and any two compatibly oriented embeddings 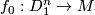 and
and 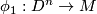 , that
, that 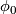 is isotopic to
is isotopic to  .
.
If  and
and  are oriented manifolds the connected sum
are oriented manifolds the connected sum 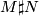 is a well-defined up to diffeomorphism. Note that orientation matters! The canoical example is
is a well-defined up to diffeomorphism. Note that orientation matters! The canoical example is
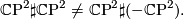
The manifolds are not even homotopy equivalent: the first has signature 2 the other signature 0. The following elementary lemma is often useful to remember.
Lemma 2.1.
Let  and
and  be locally oriented manifolds such that
be locally oriented manifolds such that  there is a diffeomoprhism
there is a diffeomoprhism 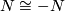 , then
, then 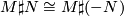 .
.
3 Connected sum along k-spheres
We say above that to define connected sum for connected k-manifolds  and
and  it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreove, the disjoint union
it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreove, the disjoint union  is the unique thickening of
is the unique thickening of 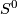 . This motivates the following
. This motivates the following
Defintion 3.1.
An 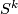 -oriented manifold is a pair
-oriented manifold is a pair 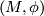 where
where  is a compact connected manifold and
is a compact connected manifold and 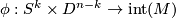 is an embedding.
is an embedding.
Defintion 3.2.
Let 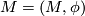 and
and 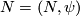 by
by 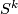 -oriented manifolds. Define
-oriented manifolds. Define
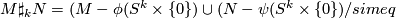
where 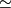 is defined via the embeddings
is defined via the embeddings 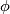 and
and 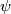 .
.
Is is clear that we have the following
Observation 3.3.
The diffeomorphism type of 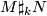 depends only upon the the isotopy classes of the embeddings
depends only upon the the isotopy classes of the embeddings 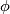 and
and 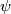 (which of course includes the diffeomorphism types of
(which of course includes the diffeomorphism types of  and
and  ).
).
4 Applications of k-sphere conneted sum
The operation of 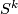 -connected sum was used in [Ajala1984] and [Ajala1987] to describe the set of smooth structures on the product of spheres
-connected sum was used in [Ajala1984] and [Ajala1987] to describe the set of smooth structures on the product of spheres 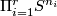 . It is also used in [Skopenkov] to define, for appropriate values of
. It is also used in [Skopenkov] to define, for appropriate values of 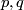 and m groups stuctures on
and m groups stuctures on 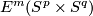 the set of smooth isotopy classes of embeddings of
the set of smooth isotopy classes of embeddings of 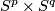 into
into  . It also appears in [Sako1981].
. It also appears in [Sako1981].
5 Parametric connected sum along thickenings
Let  be a stable fibred vector bundle. A foundational theorem of modified surgery is
be a stable fibred vector bundle. A foundational theorem of modified surgery is
In particular, 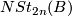 has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in [Kreck1985, Chapter 2, pp 26-7] where it is shown how to use parametric connected sum along thickenings to define an addition of stable diffeomorphism classes of close 2n-B-manifolds.
has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in [Kreck1985, Chapter 2, pp 26-7] where it is shown how to use parametric connected sum along thickenings to define an addition of stable diffeomorphism classes of close 2n-B-manifolds.
6 References
- [Ajala1984] S. O. Ajala, Differentiable structures on products of spheres, Houston J. Math. 10 (1984), no.1, 1–14. MR736571 (85c:57032) Zbl 0547.57026
- [Ajala1987] S. O. Ajala, Differentiable structures on a generalized product of spheres, Internat. J. Math. Math. Sci. 10 (1987), no.2, 217–226. MR886378 (88j:57028) Zbl 0627.57022
- [Hirsch] Template:Hirsch
- [Kreck1985] M. Kreck, An extension of the results of Browder, Novikov and Wall about surgery on compact manifolds, preprint Mainz (1985).
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Sako1981] Y. Sako, Connected sum along the cycle operation of
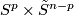 on
on  -manifolds, Proc. Japan Acad. Ser. A Math. Sci. 57 (1981), no.10, 499–502. MR640259 (83a:57043) Zbl 0505.57010
-manifolds, Proc. Japan Acad. Ser. A Math. Sci. 57 (1981), no.10, 499–502. MR640259 (83a:57043) Zbl 0505.57010
- [Skopenkov] Template:Skopenkov
|
This page has not been refereed. The information given here might be incomplete or provisional. |