Oriented bordism
(Created page with '== Introduction == <wikitex>; By the Pontrjagin-Thom isomorphism the oriented bordism groups $\Omega_n^{SO}$ of closed oriented mani…') |
(→Generators) |
||
| Line 16: | Line 16: | ||
$\Omega_4^{SO}=\Zz$, generated by the complex projective space $\CP^2$. | $\Omega_4^{SO}=\Zz$, generated by the complex projective space $\CP^2$. | ||
| − | $\ | + | $\Omega_5^{SO}=\Zz_2$, generated by the Wu manifold. |
| − | $ | + | $\Omega_6^{SO}=\Omega_7^{SO}=0$. |
$\Omega_*^{SO}\otimes \Qq$ is a polynomial ring, with generators $\CP^{2i}$. | $\Omega_*^{SO}\otimes \Qq$ is a polynomial ring, with generators $\CP^{2i}$. | ||
Revision as of 21:24, 2 February 2010
Contents |
1 Introduction
By the Pontrjagin-Thom isomorphism the oriented bordism groups 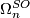 of closed oriented manifolds are isomorphic to the homotopy groups of the Thom spectrum
of closed oriented manifolds are isomorphic to the homotopy groups of the Thom spectrum  .
.
2 Generators
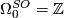 , generated by a point.
, generated by a point.
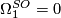 , as circles bound disks.
, as circles bound disks.
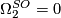 , as oriented surfaces bound handlebodies.
, as oriented surfaces bound handlebodies.
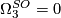 .
.
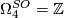 , generated by the complex projective space
, generated by the complex projective space 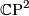 .
.
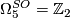 , generated by the Wu manifold.
, generated by the Wu manifold.
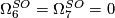 .
.
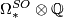 is a polynomial ring, with generators
is a polynomial ring, with generators 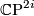 .
.
3 Invariants
Signature. Pontryagin numbers. Stiefel-Whitney numbers.
4 Classification
Thom [Thom1954] computed 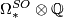 . This is equivalent to the computation of the rational (co)homology of
. This is equivalent to the computation of the rational (co)homology of 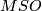 (see for the isomorphism). The cohomology
(see for the isomorphism). The cohomology 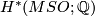 is a polynomial ring with generators the
Pontryagin classes, so that Pontryagin numbers give an additive isomorphism.
Milnor, Rohlin, Wall[Wall1960]
is a polynomial ring with generators the
Pontryagin classes, so that Pontryagin numbers give an additive isomorphism.
Milnor, Rohlin, Wall[Wall1960]
5 Further topics
6 References
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Wall1960] C. T. C. Wall, Determination of the cobordism ring, Ann. of Math. (2) 72 (1960), 292–311. MR0120654 (22 #11403) Zbl 0097.38801
|
This page has not been refereed. The information given here might be incomplete or provisional. |